Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 18.Questões e Problemas - Ex. 28
Calcule o tempo necessário para uma corrente de depositar de
como:
(a) cobalto elementar na superfície do c��todo.
(b) em um ânodo.
Considere 100% de eficiência da corrente para ambos os casos.
Passo 1
Combinaremos duas equações para calcular o tempo necessário para depositar duas espécies notadas.
A primeira equação que vamos usar para calcular o número de íons é:
Relação entre mols e massa:
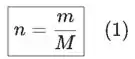
onde n é o número de mols, m é a massa e M é a massa molar.
A segunda equação que vamos usar é:
Relação entre mols e corrente elétrica:
onde I é a corrente elétrica, t é o tempo, z é a carga de um íon e F é a constante de Faraday.
Agora podemos prosseguir no cálculo do tempo. Insira a equação (1) na equação (2):
- Insira os dados fornecidos na equação (3) da etapa 4 e calcule o tempo necessário para depositar o cobalto:
- Nesta tarefa, precisamos calcular o tempo necessário para depositar . Primeiro, podemos escrever a reação de deposição de de :
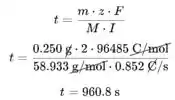
Podemos converter segundos em minutos usando a taxa de conversão entre parênteses (1 min = 60 s):
Passo 2
Antes de listarmos os dados fornecidos, podemos calcular a massa de da massa de usando sua razão de mols:
Passo 2
Insira os dados fornecidos na equação (3) do passo 4 e calcule o tempo necessário para depositar
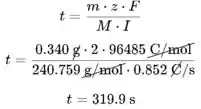
Podemos converter segundos em minutos usando a taxa de conversão entre parênteses (1 min = 60 s):