Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 11.Problemas Numéricos - Ex. 16
Para os polienos conjugados monocíclicos, com cada um dos N átomos de carbono contribuindo com um elétron num orbital 2p, a teoria simples de Hückel fornece a seguinte expressão para as energias dos orbitais moleculares .
(a) Calcule as energias dos orbitais moleculares do benzeno e do ciclooctatetraeno. Compare sobre a presença ou não de níveis de energia degenerados. (b) Calcule e compare as energias de deslocalização do benzeno (usando a expressão acima) e do hexatrieno (ver problema 11.15ª). O que você conclui dos seus resultados?
Passo 1
(a) A ausência de valores numéricos de e , nós expressamos as energias do orbital como em propósito de comparação. Lembrando que é negativo, logo o orbital com o maior valor será dado quando tiver a menor energia. Vamos então fazer uma tabelinha abaixo com a seguinte equação:
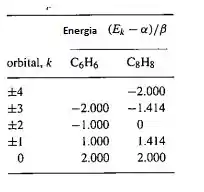
Em cada caso, o maior e menor nível de energia são dos carinhas não degenerados, enquanto os outros níveis são dos duplamente degenerados.
Passo 2
(b) A energia total de um sistema de elétron é a soma das energias dos orbitais ocupados ponderados pelo número de elétrons que os ocupa. No , cada um dos três primeiros orbitais é duplamente ocupado, mas o segundo nível é duplamente degenerado, portanto:
A energia de deslocalização é a diferença entre essa quantidade e aquela referente às 3 ligações duplas isoladas.
Para o hexatrieno linear, a energia de deslocalização é , portanto o benzeno tem consideravelmente maior energia de deslocalização. E isso mostra pra gente do porquê o benzeno ser mais estável e os aromáticos em gerais apresentarem um determinado grau de estabilização de seus anéis.
Resposta
Ei, a resposta está no passo a passo :)