Problema Desafiador. No Exemplo 10-5, negligenciamos a contribuição do ácido nitroso para a força iônica. Também usamos a solução simplificada para a concentração de íons hidrônio,
Passo 1
Neste exercício, precisamos considerar o exercício apresentado no Exemplo 10-5 , onde a constante de dissociação ácida real do ácido nitroso foi determinada considerando a atividade das soluções, não apenas as concentrações. No exercício mencionado, a concentração de prótons foi determinada pela seguinte fórmula:
a) Nesta parte, devemos realizar os cálculos feitos no exercício de exemplo mencionado novamente. Ou seja, precisamos calcular valor nas seguintes etapas:
Determinando o valor da força iônica dada pelo sal
Determinação do coeficiente de atividade das respectivas espécies pela equação de Debye-Hückel
Recalculando o valor da constante de dissociação ácida considerando também os coeficientes de atividade
Determinando a concentração de prótons presente na solução
O valor de concentração de prótons pode nos ajudar:
recalcular a força iônica , agora neste caso considerando o fato de que o ácido também se dissocia em íons
a força iônica corrigida é então novamente usada para recalcular os coeficientes de atividade , então
a constante de dissociação ácida , e
por último a concentração de prótons também
Como resultado, chegamos mais perto da concentração real de prótons do que no caso em que desprezamos a presença da atividade dos íons.
No final, precisamos calcular o erro relativo em relação ao resultado anterior e manter o recálculo (iterar) o resultado até que o erro relativo de dois resultados consecutivos fique abaixo 0.1%. No final, também precisamos calcular o erro relativo em relação ao nosso primeiro valor calculado e comparado ao valor quando a presença das atividades foi desprezada .
Passo 2
Então, vamos calcular a força iônica , inicialmente desprezando o fato de que o ácido também se dissocia. A força iônica - no caso de um composto com um único cátion positivo e um único ânion negativo - é calculada da seguinte forma:
Vamos também realizá-lo e resumir os dados em uma planilha.
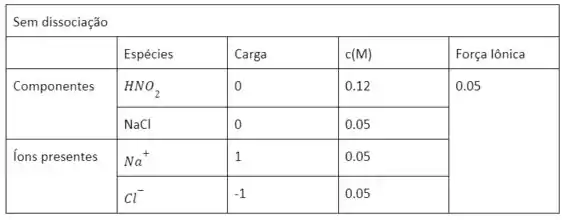
Vamos usar a equação de Debye-Hückel para determinar o coeficiente de atividade na força iônica dada.
onde Z é a carga da espécie, μ é a força do íon e α é o diâmetro efetivo do íon hidratado em nanômetros. O coeficiente de atividade de uma molécula não dissociada é 1, de modo que o do ácido nitroso será 1. O α dos íons é extraído da Tabela 10-2. Vamos demonstrar o cálculo para um dos íons e deixar o software fazer o mesmo com o restante deles, usando a mesma fórmula.
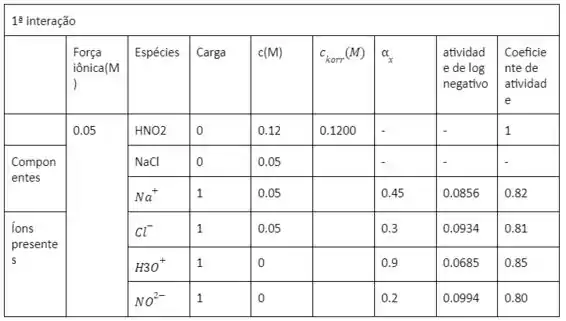
Os resultados dos cálculos realizados pela planilha estão indicados a seguir.
Representa a concentração da espécie considerando a dissociação do ácido nitroso (agora em branco, pois é negligenciado nesta etapa). O coeficiente de atividade do ácido não dissociado é 11, e o do cloreto de sódio não dissociado não está escrito, pois todo o sal se dissocia.
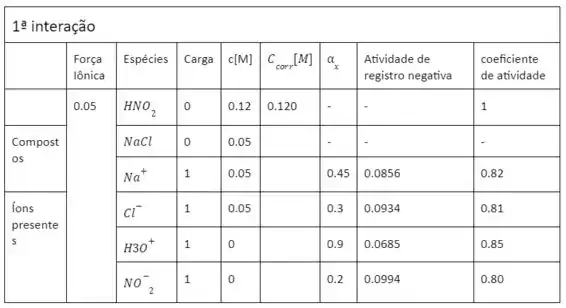
A partir dos coeficientes de atividade, devemos agora recalcular a constante de dissociação ácida.
A concentração de hidrônio deve ser calculada pela equação indicada na Etapa 1:
Vamos também calcular este valor pelo original valor para que possamos determinar o erro relativo desse valor:
A fórmula usada para o erro relativo percentual é dada da seguinte forma:
Vamos resumir os dados calculados novamente em uma tabela na planilha:

Nota: neste caso, e em todos os outros casos, o erro relativo refere-se ao valor relativo do valor anterior em relação ao atual.
Vamos repetir os cálculos até que o erro relativo seja menor que 0.1%. Primeiramente, vamos recalcular a força iônica. A força iônica é igual à soma da força iônica do sal, a concentração do íon hidrônio dissociado (calculado na etapa anterior) e do íon nitrito (o mesmo que para o hidrônio). Portanto, a força iônica para a segunda etapa de iteração é dada como:
O valor de para o ácido nitroso é dado como:
O valor para os íons dissociados é o mesmo que suas concentrações na etapa anterior.
Vamos executar o restante dos cálculos na planilha incluindo os coeficientes de atividade:
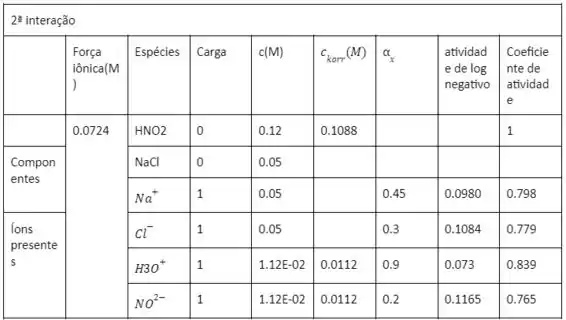
Passo 3
Vamos resumir os dados calculados novamente em uma tabela na planilha sobre a nova constante de dissociação ácida, a concentração de íons hidrônio e o erro percentual relativo:
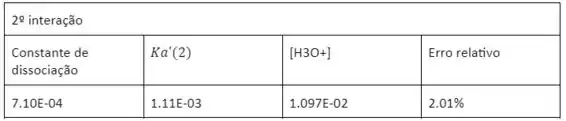
Vamos repetir os cálculos. Cada etapa é análoga às etapas da 2ª iteração. Vamos executar o restante dos cálculos na planilha incluindo os coeficientes de atividade:
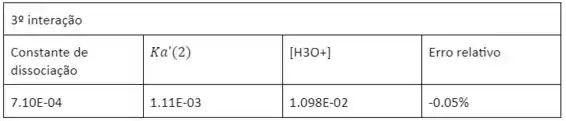
Como visto, neste caso, o erro relativo em relação ao valor da iteração anterior está dentro de 0,1%. Portanto, esta é a última etapa da iteração. Isso significa que foram necessárias 3 etapas de iterações.
No final, vamos determinar os outros valores de erro percentual relativo. O erro percentual relativo entre o último valor e o primeiro valor, onde a dissociação do ácido foi desprezada, é dado como:

O erro percentual relativo entre o último valor e o valor da primeira iteração é dado como:
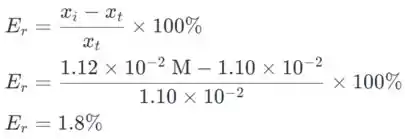
b) Nesta parte, devemos recalcular os resultados usando a fórmula quadrática em vez da fórmula mostrada no primeiro passo. Vamos deduzir a fórmula necessária, como primeiro passo
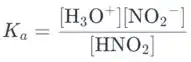
A concentração dos íons dissociados é a mesma devido à sua mesma estequiometria. Portanto, podemos substituir a concentração de íons nitrito pela concentração de íons hidrônio também:
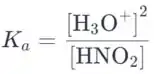
A concentração de equilíbrio de ácido nitroso é igual à concentração inicial menos a concentração do ácido nitroso dissociado. Essa quantidade também é igual à concentração de íons hidrônio devido à mesma estequiometria:
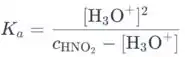
Vamos reorganizar a equação para que ela se torne adequada para a solução pela fórmula quadrática:
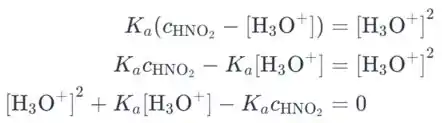
Vamos indicar a concentração de prótons como xx, por simplicidade, e substituir a concentração inicial do ácido nitroso
Indiquemos novamente a tabela contendo os cálculos do coeficiente de atividade. Nesta parte, nada mudou em relação à parte a).
Como determinamos antes, o novo valor de . Vamos usar isso para determinar a concentração de hidrônio pela fórmula quadrática. Para demonstração, os passos usados na fórmula quadrática são indicados neste caso. Vamos substituir os numerais na fórmula necessária:
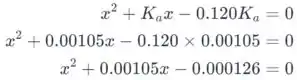
Vamos usar a fórmula quadrática para determinar x:

Como a concentração pode ser apenas um valor positivo, apenas é válido. Portanto,
Vamos também calcular esse valor com o valor também em uma planilha, pelo uso da mesma fórmula. Desta forma, podemos determinar o erro relativo desse valor de concentração de prótons também.

Conhecendo este valor sem correção de atividade, vamos indicar os valores da primeira iteração, incluindo o erro relativo do valor de concentração de prótons anterior, que é, neste caso, aquele sem correção de atividade. Depois disso, vamos repetir os cálculos até que o erro relativo esteja abaixo de



No final, vamos determinar os outros valores de erro percentual relativo. O erro percentual relativo entre o último valor e o primeiro valor, onde a dissociação do ácido foi desprezada, é dado como:

O erro percentual relativo entre o último valor e o valor da primeira iteração é dado como:
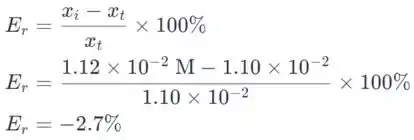
Como podemos ver, as diferenças entre as partes a) e b) foram bastante significativas nas etapas 0 e 1 da iteração, pois nesses casos a dissociação do ácido foi negligenciada. No caso das etapas de iteração adicionais (2ª e 3ª), as diferenças entre os dois valores no mesmo número de iteração tornam-se cada vez menores. Isso pode ser explicado pelo fato de que nas 2ª e 3ª iterações, na parte a), também consideramos a dissociação do ácido das iterações anteriores (por exemplo, na 2ª iteração, subtraímos a concentração de prótons produzida na primeira iteração da concentração de ácido nitroso). Isso significa que o método introduzido na parte b) produz mudanças apreciáveis nos resultados apenas nas etapas 0 e 1 da iteração.
Em suma, poderíamos dizer que a fórmula quadrática nos ajuda a encontrar resultados mais precisos apenas no caso de não corrigirmos a concentração do ácido nitroso pela concentração anterior do íon hidrônio na fórmula simplificada.
c) Nesta parte, devemos decidir quando devemos considerar a correção por coeficientes de atividade ao determinar a concentração de hidrônio de pH. Como pudemos ver nos cálculos, o efeito da força iônica tem um grande efeito no valor. Ou seja, a variável que mais deve ser considerada é a força iônica. Mais especificamente, quanto maiores as forças iônicas, mais os coeficientes de atividade se tornam diferentes de 1. Isso resultará em uma diferença maior entre e valores. Isso significa que tais correções devem ser consideradas no caso de grandes forças iônicas, como no caso de grande concentração de sal e íons de carga múltipla.
d) Nesta parte, devemos determinar quando as correções aplicadas na parte b) podem ser necessárias. Vamos indicar a determinação de em uma das etapas da Etapa 12:
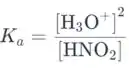
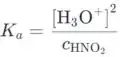
![]()
No entanto, este pode ser o caso apenas quando a concentração dos prótons dissociados é insignificante, o que ocorre no caso em que a concentração dos prótons dissociados é menor que a concentração do ácido em algumas magnitudes. Isso acontece apenas no caso de ácidos (muito) fracos. Portanto, esta simplificação pode ser usada quando o de um ácido é (muito) baixo.
e) Neste exercício, devemos decidir se as correções de atividade são possíveis em matrizes complexas como uma amostra de urina ou sangue. Isso só é possível se for possível determinar a força iônica das amostras.
No entanto, não é uma tarefa fácil. Amostras de urina e sangue contêm muitos tipos de íons com valores de carga versáteis. Para determinar a força iônica, devemos conhecer a carga dos íons e também a concentração deles. Isso pode ser possível com boa exatidão e precisão por cromatografia de íons, onde os íons interagem com a fase estacionária de acordo com sua carga e peso atômico (molecular) (a polarizabilidade do íon é a chave no caso de cargas semelhantes).
Por outro lado, alguns métodos de HPLC com detecção eletroquímica também podem nos ajudar a determinar a quantidade de íons ou espécies ionizáveis.
Resposta
Ver o desenvolvimento