Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 4.Aplicações - Ex. 20

As proteínas são polipeptídios, polímeros de aminoácidos que podem existir sob a forma de uma estrutura ordenada que é estabilizada por uma série de interações moleculares. Entretanto, sob certas condições a estrutura compacta da cadeia polipeptídica pode colapsar em uma cadeia aleatória. Essa modificação estrutural pode ser considerada como uma transição de fases com uma temperatura característica de transição, a temperatura de fusão, Tf, que aumenta com o número e a intensidade das interações intermoleculares da cadeia. Podemos fazer um tratamento termodinâmico para calcular a temperatura Tf quando um polipeptídio em forma de hélice, mantido estável por ligações hidrogênio, desdobra-se formando uma cadeia aleatória. Se um polipeptídio tem n aminoácidos, temos n — 4 ligações hidrogênio para formar uma hélice-a, a forma mais comum de estrutura helicoidal nas proteínas (veja o Cap. 19, Vol. 2). Uma vez que o primeiro resíduo e o último resíduo na cadeia têm movimentos livres, n — 2 resíduos formam uma hélice compacta e têm movimentos restritos. Baseando-se nessas ideias, pode-se escrever que a energia de Gibbs molar de desdobramento de um polipeptídio com n ≥ 5 é dada por:

∆ G m = n - 4 ∆ l h H m - ( n - 2 ) T ∆ l h S m

Onde ∆ l h H m   e   ∆ l h S m , são, respectivamente, a entalpia e a entropia molares de dissociação de ligações hidrogênio em um polipeptídio. (a) Justifique a forma da equação da energia de Gibbs de desdobramento. Isto é, por que os termos de entalpia e entropia são escritos, como n - 4 ∆ l h H m   e   ( n - 2 ) T ∆ l h S m   ? (b) Mostre que Tf pode ser escrita como

T f = n - 4 ∆ l h H m ( n - 2 ) T ∆ l h S m

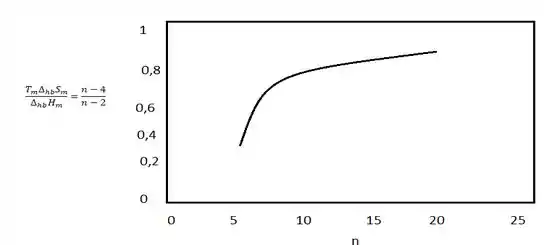
(c) Faça um gráfico de T f / ( ∆ l h H m /   ∆ l h S m ) para 5 ≤ n ≤ 20 . Para que valor de n Tf varia menos de 1% quando n aumenta de uma unidade?

Passo 1

Oi pessoal, vamos resolver essa questão?

Para a paetê (a) da questão vamos ter a seguinte justificativa:

Os termos de entalpia e entropia são escritos, como n - 4 ∆ l h H m   e   n - 2 T ∆ l h S m , pois o termo entalpia é justificado por n —4 ligações de hidrogênio independentes, para as quais cada uma requer ∆ h b H m de calor para quebrar durante a dissociação de fusão. O termo entropia é justificado por n - 2 altamente ordenado, mas independentes, estruturas para as quais cada uma experimenta um aumento de entropia de ∆ h b H m durante o processo de fusão.

Passo 2

Na parte (b) da questão vamos demonstrar que:

T f = n - 4 ∆ l h H m ( n - 2 ) T ∆ l h S m

Para isso temos que saber que:

∆ t r s S = ∆   t r s H T t r s

Logo temos que:

T t r s = ∆ t r s H ∆ t r s S

Dessa forma torna-se:

T f = n - 4 ∆ l h H m ( n - 2 ) T ∆ l h S m

Passo 3

Para a situação descrita na parte (c) da questão vamos ter um gráfico da seguinte como:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Que fração da entalpia de vaporização do etanol é consumida na expansão do seu vapor?
Calcule o ponto de fusão do gelo sob pressão de 50 bar. Admita que a massa específica do gelo, nessas condições, seja, aproximadamente, 0,92 gc m - 3 e a da água líquida 1,00 gc m - 3 .
O naftaleno, C 10 H 8 , funde-se a 80,2 °C. Se a pressão de vapor do líquido for de 1,3 KPa, a 85,8 °C e 5,3 KPa a 119,3 °C, use a equação de Clausius-Clapeyron para calcular (a) a entalpia de vaporiz
Calcule o ponto de fusão do gelo sob pressão de 10 MPa. Admita que a massa específica do gelo, nessas condições, seja, aproximadamente, 0,915 gc m - 3 e a da água líquida 0,998 gc m - 3 .
O ponto de ebulição normal do Hexano é 69,0 °C. Estime (a) a entalpia de vaporização e (b) a pressão de vapor a 25 °C e 60 °C.