Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 10.1 - Ex. 122

  1. Use gráficos padrão de computador e dados de 1000 K e 1200 K da Tabela 10.2, para lançar em gráficos as equações de van 't Hoff da dissociação dos halogênios diatômicos em seus átomos, X 2 ( g ) ↔ 2   X ( g ) .
  2. A partir dos gráficos, determine as entalpias e entropias da dissociação.
  3. Use esses dados para calcular as entropias molares dos átomos de halogênio na fase gás,   X ( g ) .

Passo 1

Bora pra mais uma !!

Então galera, a variação da energia livre de Gibbs é:

∆ G r 0 = ∆ H 0 - T ∆ S 0

No equilíbrio nós podemos relacioná-la da seguinte maneira:

∆ G r 0 = - R T l n   K

Onde K é a constante do equilíbrio e R a constante dos gases ideiais:

R = 8,314 J m o l . K

Substituindo:

- R T l n   K = ∆ H 0 - T ∆ S 0

Isolando ln K e reorganizando:

l n   K = - ∆ H 0 R 1 T + ∆ S 0 R  

Olha que legal ! Arrumamos uma equação linear onde - ∆ H 0 R é a inclinação da reta e ∆ S 0 R a interseção da reta no eixo de ln K.

Para os halogênio, de acordo com a Tabela 10.2:

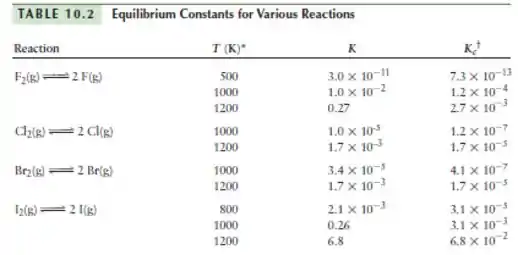
Para linearização da função:

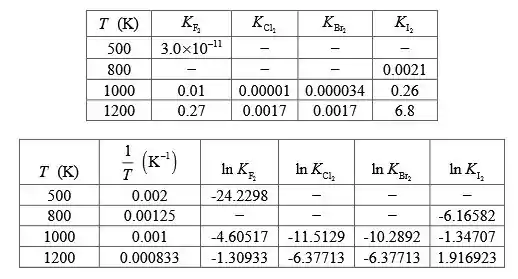
No gráfico:

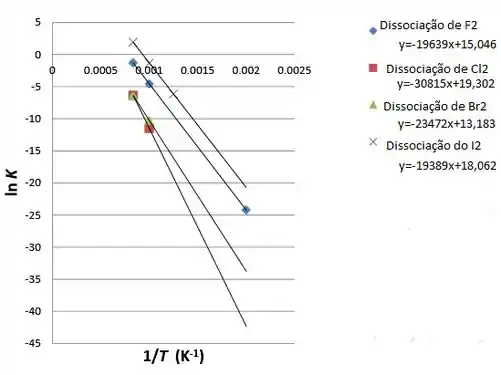
Passo 2

Começando pelo F 2 , e pela equação da reta sabemos que:

- ∆ H 0 R = - 19639   K

Substituindo R:

∆ H 0 = 19639   K 8,314 J m o l . K = 163,3 × 10 3 J m o l

Ou melhor:

∆ H 0 = 163,3 k J m o l

Para a interseção:

∆ S 0 R = 15,046

Substituindo R:

∆ S 0 = 15,046 8,314 J m o l . K = 125,1 J m o l . K

Já descobrimos a entalpia e a entropia para o gás diatômico F 2 .

Passo 3

Começando pelo C l 2 , e pela equação da reta sabemos que:

- ∆ H 0 R = - 30815   K

Substituindo R:

∆ H 0 = 30815   K 8,314 J m o l . K = 256,2 × 10 3 J m o l

Ou melhor:

∆ H 0 = 256,2 k J m o l

Para a interseção:

∆ S 0 R = 19,302

Substituindo R:

∆ S 0 = 19,302 8,314 J m o l . K = 160,5 J m o l . K

E aqui estão a entalpia e a entropia para o gás diatômico C l 2 .

Passo 4

Começando pelo B r 2 , e pela equação da reta sabemos que:

- ∆ H 0 R = - 23472   K

Substituindo R:

∆ H 0 = 23472   K 8,314 J m o l . K = 195,1 × 10 3 J m o l

Ou melhor:

∆ H 0 = 195,1 k J m o l

Para a interseção:

∆ S 0 R = 13,183

Substituindo R:

∆ S 0 = 13,183 8,314 J m o l . K = 109,6 J m o l . K

E aqui estão a entalpia e a entropia para o gás diatômico B r 2 .

Passo 5

Começando pelo I 2 , e pela equação da reta sabemos que:

- ∆ H 0 R = - 19389   K

Substituindo R:

∆ H 0 = 19389   K 8,314 J m o l . K = 161,2 × 10 3 J m o l

Ou melhor:

∆ H 0 = 161,2 k J m o l

Para a interseção:

∆ S 0 R = 18,062

Substituindo R:

∆ S 0 = 18,062 8,314 J m o l . K = 150,2 J m o l . K

E aqui estão a entalpia e a entropia para o gás diatômico I 2 .

Mas nada de acabar, não é?

Passo 6

Na letra c nós precisamos da entropia molar dos átomos de halogênio na fase gás.

Usando a lei de Hess:

∆ S 0 = ∑ m S p r o d u t o s 0 - ∑ m S r e a g e n t e s 0

A equação é do tipo:

X 2 ( g ) ↔ 2   X ( g )

Ela ficará assim:

∆ S 0 = 2 S X 0 - S X 2 0

Isolando S X 0 :

S X 0 = ∆ S 0 + S X 2 0 2

Começando por F 2 :

∆ S 0 = 125,1 J m o l . K

S F 2 0 = 202,78   J m o l . K

Sendo assim:

S F 0 = 163,9 J m o l . K

Para a fase gasosa do F 2 a entropia molar padrão é 163,9 J m o l . K .

Passo 7

Para C l 2 :

∆ S 0 = 160,5 J m o l . K

S C l 2 0 = 223,07   J m o l . K

Sendo assim:

S C l 0 = 191,8 J m o l . K

Para a fase gasosa do C l 2 a entropia molar padrão é 191,8 J m o l . K .

Para B r 2 :

∆ S 0 = 109,6 J m o l . K

S B r 2 0 = 245,46   J m o l . K

Sendo assim:

S B r 0 = 177,5 J m o l . K

Para a fase gasosa do B r 2 a entropia molar padrão é 177,5 J m o l . K .

E finalizamos com I 2 :

∆ S 0 = 150,2 J m o l . K

S I 2 0 = 2 60,69   J m o l . K

Sendo assim:

S I 0 = 205,4 J m o l . K

Para a fase gasosa do I 2 a entropia molar padrão é 205,4   J m o l . K .

Ufaaa! Essa foi bem grande, mas acabamooos !!

Resposta

  2. F 2 :   ∆ H 0 = 163,3 k J m o l | ∆ S 0 = 125,1 J m o l . K ;

    3. C l 2 :   ∆ H 0 = 256,2 k J m o l | ∆ S 0 = 160,5 J m o l . K ;

    B r 2 :   ∆ H 0 = 195,1 k J m o l | ∆ S 0 = 109,6 J m o l . K ;

    I 2 :   ∆ H 0 = 161,2 k J m o l | ∆ S 0 = 150,2 J m o l . K ;

  3. S F 0 = 163,9 J m o l . K ;

S C l 0 = 191,8 J m o l . K ;

S B r 0 = 177,5 J m o l . K ;

S I 0 = 205,4 J m o l . K .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual a entalpia-padrão de reação de uma reação cuja constante de equilíbrio (a) é duplicada, (b) é dividida por dois, quando a temperatura aumenta de 10K a partir de 298K ?
A pressão de vapor da dissociação do N H 4 C I , a 427° C , é 608k P a , e é 1115k P a a 459° C . Calcule (a) a constante de equilibrio, (b) a energia de Gibbs padrão da reação, (c) a entalpia-padrão,
A energia de Gibbs padrão de formação doN H 3 ( g ) é -16,5k J.m o l - 1 a 298K . Qual a energia de Gibbs da reação quando as pressões parciais do N 2 , do H 2 , e do N H 3 , (tratados como gases perf
Estime a temperatura em que o C u S O 4. 5 H 2 O sofre desidratação.
A constante de equilíbrio da reação N 2 ( g ) + O 2 ( g ) ⇌ 2N O ( g ) é 1,69 × 10 - 3 a 2300K . Uma mistura de 5,0g de nitrogênio e 2,0g de oxigênio está encerrada num recipiente de 1,0d m 3 e é aque