Neste problema, vamos examinar aspectos cinéticos da hidrólise de N-glutaril-L-fenilalanina-p-nitroanilida (GPNA) que resulta na formação de p-nitroanilina e N-glutaril-fenilalanina. Além disso, recebemos informações de que a reação segue a cinética de Michaelis-Menten nos estágios iniciais.

1. A primeira tarefa é transformar a equação de Michaelis-Menten na equação de Lineweaver-Burke.

Conforme instruído no problema, vamos começar da equação 29-19, que é a equação de Michaelis-Menten:

Em primeiro lugar, vamos eliminar e , porque sabemos que essas duas variáveis ​​quando multiplicadas dão a taxa máxima de reação da reação enzimática:

2. Agora, vamos usar a equação Lineweaver-Burke da tarefa acima para determinar os seguintes parâmetros cinéticos



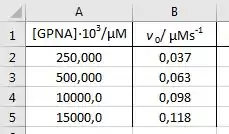
Para construir o gráfico Lineweaver-Burke, temos que manipular os dados fornecidos como mostrado na figura abaixo:



O próximo passo é traçar o valor recíproco da concentração do substrato contra o valor recíproco da taxa de reação inicial:



Observando a equação de Lineweaver-Burke, você pode ver que a inclinação da equação corresponde à razão entre a constante de Michaelis e a taxa de reação máxima, enquanto a interceptação corresponde ao valor recíproco da taxa de reação máxima:



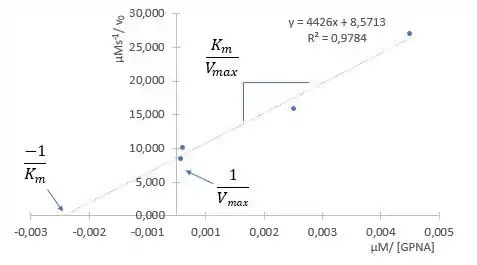
A constante de Michaelis e a taxa máxima de reação são calculadas a partir da equação do gráfico acima:

A inclusão de valores conhecidos na equação acima fornece:

Passo 2

3. Para resolver esse problema, usaremos uma lógica semelhante à de (b). Começamos com a equação de Michaelis-Menten:

Para determinar os parâmetros cinéticos, , e , usando a equação de Hannes-Woolf, primeiramente, temos que manipular os dados fornecidos no problema conforme mostrado na figura abaixo:



O próximo passo é traçar a razão entre a concentração do substrato e a taxa de reação inicial em relação à concentração do substrato:



Observando a equação de Hannes-Woolf, você pode ver que a inclinação do gráfico corresponde ao valor recíproco da taxa de reação máxima, enquanto a interseção da linha do gráfico com o eixo x corresponde ao valor negativo da constante de Michaelis:



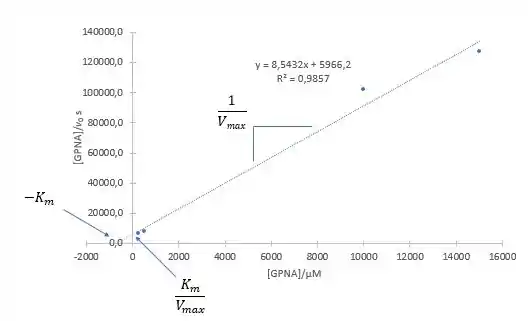
A constante de Michaelis e a taxa máxima de reação são calculadas a partir da equação do gráfico acima:

Número de faturamento ( ) é calculado pela equação:

Passo 3

4. Para resolver esse problema, usaremos uma lógica semelhante à de (b) e (c). Começamos com a equação de Michaelis-Menten:

Para determinar os parâmetros cinéticos, , usando a equação de Eadie-Hofstee, primeiramente, temos que manipular os dados fornecidos no problema conforme mostrado na figura abaixo:



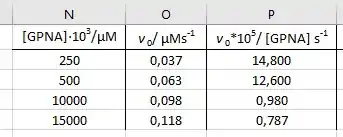
O próximo passo é traçar a razão entre a taxa de reação inicial e a concentração de substrato em relação à taxa de reação inicial:



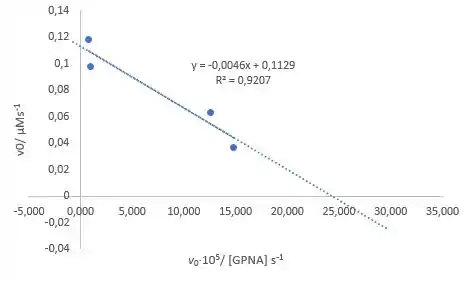
Observando a equação de Eadie-Hofstee, você pode ver que a inclinação da equação corresponde ao valor negativo da constante de Michaelis, enquanto a interceptação com o eixo y corresponde à taxa máxima de reação:



A constante de Michaelis e a taxa máxima de reação são calculadas a partir da equação do gráfico acima:

A inclusão de valores conhecidos na equação acima fornece:

5. A partir dos gráficos acima, você pode ver que os pontos no gráfico de Eadie-Hofstee se desviam mais da linha de regressão, o que pode ser explicado pelo fato de que ambos os eixos dependem da taxa de reação e, portanto, haverá um erro experimental em ambos os eixos.

Além disso, você pode ver que e os valores são muito diferentes dos valores determinados pelos gráficos de Lineweaver-Burke e Hannes-Woolf.

Por outro lado, a inclinação do gráfico no gráfico de Lineweaver-Burke depende muito da concentração inicial e dos pontos que estão distantes da origem, o que resulta em um erro na determinação dos parâmetros cinéticos.

Portanto, Hannes-Woolf seria mais preciso na determinação dos parâmetros cinéticos.

6. Como sabemos que as amostras foram analisadas nas mesmas condições da parte (b), usaremos a equação de Lineweaver-Burke calculada em (b) para obter as concentrações [GPNA]:

Conectando os dados fornecidos no problema na equação superior dá: