Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 29.Questões e Problemas - Ex. 10gh
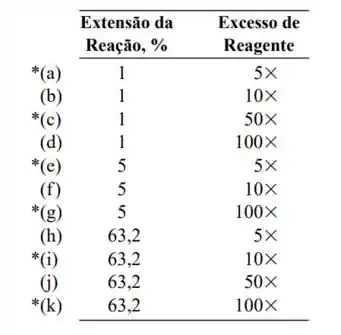
Encontre o erro relativo associado com a hipótese de que k’ não varia no decorrer de uma reação de pseudoprimeira ordem sob as seguintes condições.
Passo 1
E ai meus queridos? Tudo certinho?
“Operador! Me dê o número do responde ai!.... Preciso resolver essa questão”
A nossa fórmula de erro relativo é expressa da seguinte maneira
Passo 2
- Extensão de reação 5
Concentração de vezes mais do que
Considerando a seguinte reação
A concentração inicial do reagente é dada como
Com 5% de reação, 95% de A permanece
Desta maneira
A taxa de reação de 5% sob a condição de pseudo-condição de primeira ordem é dada como
é a taxa na reação de 5% e a taxa medida será:
Passo 3
Vamos substituir os valores na fórmula do erro relativo, portanto
Portanto, o erro relativo da reação dada é de
Passo 4
- Extensão de reação
Concentração de vezes mais do que
Considerando a seguinte reação
A concentração inicial do reagente é dada como
Com 63.2% de reação, 36.8% de A permanece
Desta maneira
A taxa de reação de 63.2% sob a condição de pseudo-condição de primeira ordem é dada como
é a taxa na reação de 63.2% e a taxa medida será:
Passo 5
Vamos substituir os valores na fórmula do erro relativo, portanto
Portanto, o erro relativo da reação dada é de
"Se algo é difícil de fazer, vale a pena ser feito!"
Resposta
g) Portanto, o erro relativo da reação dada é de
h) Portanto, o erro relativo da reação dada é de