Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Potenciais Termodinâmicos

Ver Todos os Exercícios

Teoria

E aeee… como andas? Vamos dar aquela estudada em potenciais termodinâmicos? Bora!!

Mas o que é o potencial termodinâmico?

Ele diz pra gente, quantitativamente, se é possível um sistema sofrer transformação… É o seguinte, ele pode nos mostrar se uma transformação é reversível ou irreversível, entendeu?

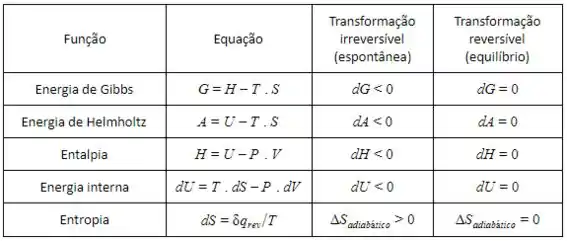
O mais interessante é que a forma de calcular ele é exatamente a aplicação de um critério de equilíbrio… Existem diferentes funções termodinâmicas para isso, quer ver?

  • Entropia (S)
  • Entalpia (H)
  • Energia interna (U)
  • Energia Livre de Gibbs (G)
  • Energia livre de Helmholtz (A)

Essa galera toda aí é um potencial termodinâmico em determinadas condições, beleza?

Vamos listar essas condições pra gente não esquecer: No caso da entropia precisamos de um processo adiabático, na entalpia precisamos de pressão constante, já no caso da energia interna precisamos de volume constante, agora na energia livre de Helmholtz precisamos de volume e temperatura constantes e pra fechar na energia livre de Gibbs precisamos de pressão e temperatura constantes.

A gente já teve contato com essas funções antes, em algum lugar, né?

Mas não custa nada relembrar não é mesmo… Então vamos fazer um resumão da forma de calcular cada um e dos seus critérios para identificar transformações reversíveis e irreversíveis, beleza?

Se liga no nosso quadrinho:

Propriedades Fundamentais dos Potenciais Termodinâmicos

Temos três propriedades fundamentais para termos um potencial termodinâmico:

  1. Continuidade: O potencial deve ser uma função contínua e diferenciável, em todas as variáveis do espaço.
  2. Extensividade: O potencial termodinâmico é uma função extensiva que possui variáveis extensivas.
  3. Convexidade: O potencial é uma função convexa, analisando o conjunto de variáveis extensivas e uma função côncava analisando o conjunto campos termodinâmicos.

Show de bola, né? Basicamente esse assunto é um grande resumo de outros assuntos ue já estudamos!

Agora partiu fazer exercícios e…

Exercícios Resolvidos

Exercício Resolvido #1

Universidade Estadual de Goiás - Lista de Físico Química II

Quais são as variáveis naturais dos potenciais termodinâmicos U , H , A e G ?

Passo 1

Bem, o nosso enunciado ta perguntando as variáveis desses potenciais termodinâmicos aí, mas vamos relembrar quem são eles antes, né?

U : Energia interna H : Entalpia A : Energia de Helmholtz G : Energia de Gibbs

Show! Agora vamos então relembrar as variáveis de cada um deles:

Energia interna: calor e trabalho

Entalpia: energia interna, pressão e volume

Energia de Helmholtz: energia interna, entropia e temperatura.

Energia Gibbs: entalpia, temperatura e entropia.

Prontinho!

Resposta

U : calor e trabalho

H : energia interna, pressão e volume

A : energia interna, entropia e temperatura.

G : entalpia, temperatura e entropia.

Exercício Resolvido #2

Universidade Estadual de Goiás - Lista de Físico Química II

Qual a condição termodinâmica para a espontaneidade dos processos químicos?

Passo 1

Precisamos verificar, entre os nossos potenciais termodinâmicos quais são os critérios que define a espontaneidade das transformações químicas, ok?

Vamos lá então! Se estamos falando que entalpia, nosso critério é Δ H < 0 , se for entropia Δ S a d i a b á t i c o > 0 , se energia interna Δ U < 0 , agora se for energia de Helmholtz temos que ter Δ A < 0 e por fim, se estivermos avaliando a energia livre de Gibbs Δ G < 0 .

Tranquilo? Show de bolinhas!

Resposta

Exercício Resolvido #3

Instituto politécnico de Tomar - Termodinâmica Química

A capacidade calorífica molar, a 1   a t m , do magnésio sólido, entre 0 ° C e 600 ° C é dada por:

c p ( J / m o l . K ) = 26,0 + 5,46   .   10 - 6   .   T - 28,6   .   10 4   .   T - 2

Calcular a variação de entropia quando 1   m o l de metal é aquecido desde 27 ° C a 227 ° C a 1   a t m .

Passo 1

Bem, o nosso enunciado pediu a variação de entropia, Δ S , tranquilo?

Antes de começar com as continhas vamos anotar os nossos dados:

n = 1   m o l p = 1   a t m T 1 = 27 ° C → 300   K

T 2 = 227 ° C → 500   K c p ( J / m o l . K ) = 26,0 + 5,46   .   10 - 6   .   T - 28,6   .   10 4   .   T - 2

Agora vamos as continhas!

Passo 2

A variação de entropia tem alguns jeitos de calcular, aí a gente pode se basear nos dados do problema… No nosso caso vamos calcular assim, olha só:

Δ S = ∫ T 1 T 2 c p , T . d T

Δ S = ∫ 300 500 26,0 + 5,46   .   10 - 6   .   T - 28,6   .   10 4   .   T - 2 T . d T

Δ S = ∫ 300 500 26,0 T + 5,46   .   10 - 6 - 28,6   .   10 4 T 3   . d T

Δ S = ∫ 300 500 26,0 T . d T + ∫ 300 500 5,46   .   10 - 6 . d T - ∫ 300 500 28,6   .   10 4 T 3   . d T

Δ S = 26   .   l n 500 - l n 300 + 5,46   .   10 - 6   .   500 - 300 - 28,6   .   10 4   .   - 1 2   .   500 ² - - 1 2   .   300 ²

Δ S = 13,28 + 0,00109 - 1,017

Δ S = 12,26   J / m o l . K

Show de bola! Conseguimos!!

Resposta

Δ S = 12,26   J / m o l . K

Exercício Resolvido #4

Universidade Federal do ABC - Fenômenos Térmicos - 4ª Lista de exercícios

Medidas calorimétricas mostram que a variação da entropia na oxidação do ferro em F e 2 O 3 sólido é de Δ S =   - 272   J / K . m o l . Esse processo ocorre espontaneamente à 20 ° C ? A entalpia de formação de um mol de óxido de ferro no processo é de Δ H =   - 824,2   k J / m o l .

Passo 1

Olha só, nosso enunciado quer saber se esse processo ocorre espontaneamente a uma temperatura de T = 20 ° C → 293   K , beleza?

Uma forma da gente descobrir isso é verificando o critério de espontaneidade de um potencial termodinâmico conhecido nosso: A energia livre de Gibbs.

Temos que verificar se Δ G < 0 , vamos nessa!

Passo 2

Calculando nosso Δ G , temos:

Δ G = Δ H - T   .   Δ S

Δ G = - 824,2   .   10 3 - 293   .   - 272

Δ G =   - 744,5   .   10 3   J / m o l

ou

Δ G =   - 744,5   k J / m o l

Opa! Nossa energia livre de Gibbs é menor que zero então esse processo, a essa temperatura, é sim espontâneo!!

Arrasamos!

Resposta

Sim, esse processo ocorre espontaneamente, pois Δ G < 0 .

Exercício Resolvido #5

Adaptado de Universidade de São Paulo - Físico Química

Calcular a variação de entropia e a variação da energia livre de Gibbs quando um átomo-grama de C u super resfriado a 1340   K solidifica irreversivelmente nesta temperatura a 1   a t m de pressão. Dados:

c p   ( s ) = 5,41 + 1,5   .   10 - 3   .   T   ( c a l / a t g . K ) ;

c p   ( l ) = 7,5   c a l / a t g . K ;

H s → l   =   3100   c a l / a t g ;

T s → l =   1356   K .

Passo 1

Vamos arrasar nessa questão!

Vamos começar separando o que nos foi dado e o que foi pedido, pra gente não se enrolar, beleza?

T = 1340   K p = 1   a t m c p   ( s ) = 5,41 + 1,5   .   10 - 3   .   T   ( c a l / a t g . K )

c p   ( l ) = 7,5   c a l / a t g . K H s → l   =   3100   c a l / a t g T s → l =   1356   K

Δ S = ? Δ G = ?

Agora sim! Partiu continhas!

Passo 2

Vamos começar dando uma olhada na forma de se calcular as duas coisas e depois escolhemos qual vai primeiro, ok?

A variação de entropia tem várias maneiras de se obter de acordo com os dados fornecidos em cada problema, aqui vamos colocar uma fórmula para esse tipo de problema, tranquilo?

Δ S = ∫ T 1 T 2 c p ,   l T . d T + Δ H T + ∫ T 2 T 1 c p ,   s T . d T

Já a variação de energia livre de Gibbs, vamos usar a clássica equação:

Δ G = Δ H - T   .   Δ S

Já vimos que precisamos encontrar primeiro a variação de entropia, né?

E além disso, será preciso encontrar o Δ H C u …. Vamos nessa!

Passo 3

Temos todos os dados então ficaremos com:

Δ S = ∫ 1340 1356 c p ,   l T . d T + - 3100 1356 + ∫ 1356 1340 c p ,   s T . d T

Δ S = c p ,   l   .   ∫ 1340 1356 1 T . d T + - 3100 1356 + c p ,   s   .   ∫ 1356 1340 1 T . d T

Δ S = c p ,   l   . l n T | 1340 1356 + - 3100 1356 + c p ,   s   .   l n T | 1356 1340

Δ S = 7,5   .   l n 1356 - l n 1340 + - 3100 1356 + 5,41 + 1,5   .   10 - 3   .   1340   .   l n 1340 - l n 1356

Δ S = 0,089 - 2,286 - 0,088

Δ S =   - 2,285   c a l / K

Show de bola, já resolvemos a primeira parte! Agora vamos encontrar a entalpia para conseguir calcular a energia livre de Gibbs.

Passo 4

Vamos achar a entalpia com a seguinte equação:

Δ H C u = Δ H + ∫ T 1 T 2 Δ c p . d T

Δ H C u = Δ H + ∫ T 1 T 2 c p ,   s - c p ,   l . d T

Δ H C u =   - 3100 + ∫ 1356 1340 5,41 + 1,5   .   10 - 3   .   T - 7,5 . d T

Δ H C u =   - 3100 + 5,41 . T + 1,5   .   10 - 3   .   T 2 2 - 7,5 . T | 1356 1340

Δ H C u =   - 3098,91   c a l / m o l

Beleza!

Passo 5

Agora pra finalizar vamos achar a energia livre de Gibbs!

Δ G =   - 3098,91 - 1340   .   - 2,285

Δ G =   - 37,01   c a l / m o l

Uhul! Arrasamos!!

Resposta

Δ S =   - 2,285   c a l / K Δ G =   - 37,01   c a l / m o l