Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Relações de Maxwell

Ver Todos os Exercícios

Teoria

As relações de Maxwell são um conjunto de equações diferenciais que relacionam várias propriedades termodinâmicas umas com as outras. Elas são cruciais para derivar relações entre variáveis termodinâmicas, como a energia interna e entalpia e nos permite calcular mudanças nessas variáveis com base em outras variáveis termodinâmicas, como temperatura e pressão.

📢 Clique para ver mais:

Na prática as relações de Maxwell nos ajuda a calcular propriedades que não podem ser medidas experimentalmente! Bora conhecer esses carinhas? 🤩🤩🤩

Relações de Maxwell: Energia Interna

A derivada da energia interna é dada pela seguinte equação:

Primeiro vamos pegar os casos mais simples, na primeira equação se tivermos o volume constante o termo pdv se torna nulo, pois a derivada de uma constante é nula. Então, teremos que:

Podemos fazer a mesma coisa para um processo com entropia constante e teríamos que:

Nesses dois exemplos seguimos o mesmo raciocínio de manter uma variável constante e aplicar a derivada fazendo com que essa variável se anule e a relação apareça. Existe uma outra forma de achar diferentes relações onde:

Aí agora é só fazer a substituição:

Relações de Maxwell: Entalpia

A derivada da entalpia é dada pela seguinte equação:

Vamos seguir o mesmo passo-a-passo do tópico anterior, mantendo a entropia constante vamos obter:

E no caso da pressão constante:

Substituindo em com e vamos ter:

Relações de Maxwell: Função de Helmholtz

A função de Helmholtz (A) é definida como a energia interna menos o produto da temperatura pela entropia.

Se aplicarmos o diferencial na equação vamos ter o seguinte:

Que pode ser simplificada, utilizando a derivada da energia interna. Assim ficamos com:

Vamos seguir o mesmo passo-a-passo que vimos acima, mantendo a temperatura constante vamos obter:

E no caso do volume constante:

Utilizando a definição de derivada exata com e vamos ter:

Relações de Maxwell: Função de Gibbs

A função de Gibbs , é definida como a entalpia menos o produto da temperatura pela entropia.

Se aplicarmos o diferencial na equação vamos ter o seguinte:

Que pode ser simplificada, utilizando a derivada da entalpia:

Vamos seguir o mesmo passo-a-passo, mantendo a temperatura constante vamos obter:

E no caso da pressão constante:

Utilizando a substituição:

Onde e vamos ter:

Relações de Maxwell: Resumo

Agora pra acabar, se liga nesse resumo com todas as relações de Maxwell que você precisa saber

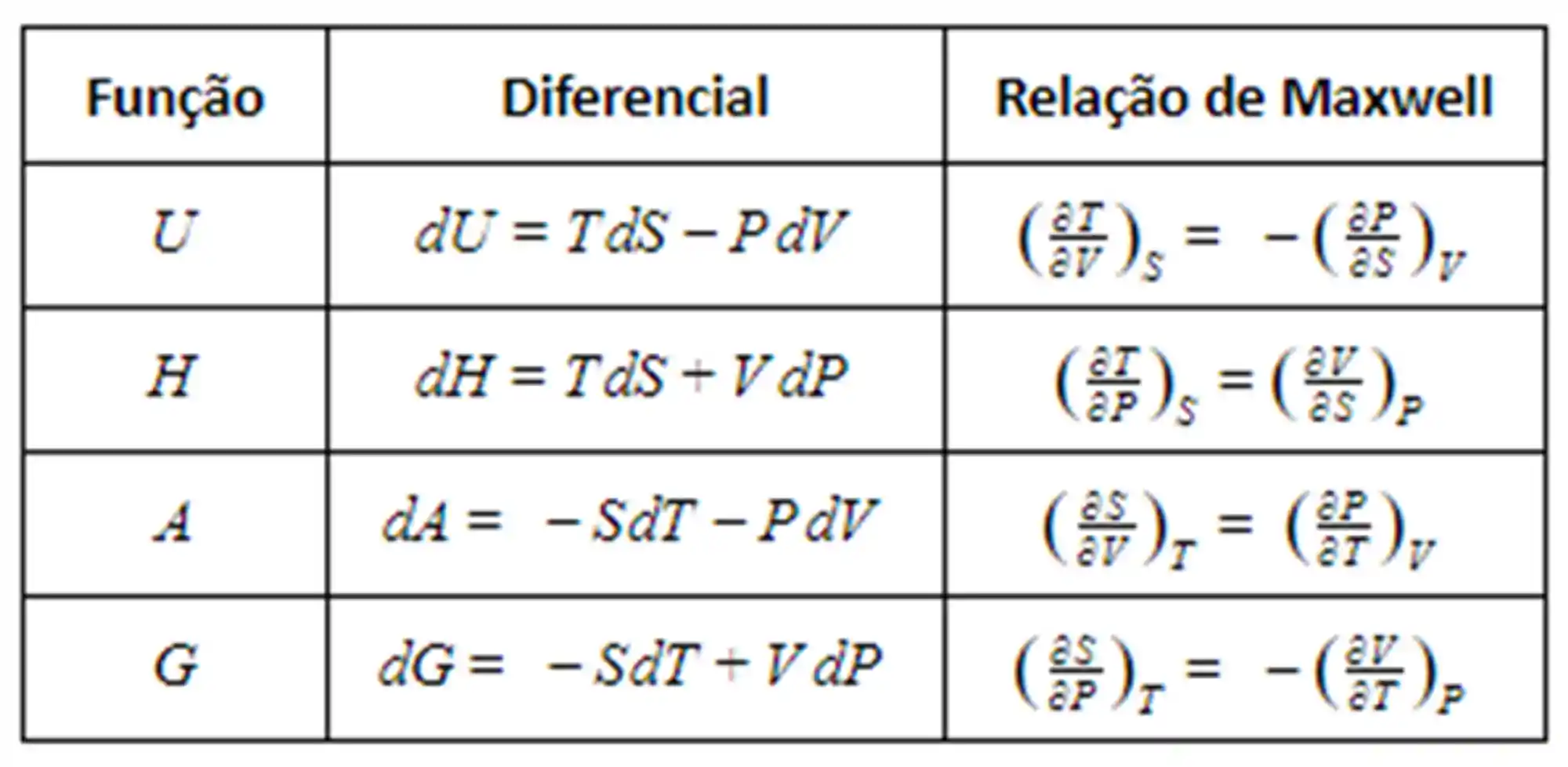
Relações de Maxwell: Resumo
Relações de Maxwell: Resumo

Agora vamos praticar com exercícios?

Relações de Maxwell: Entalpia

Relações de Maxwell: Função de Helmholtz

Relações de Maxwell: Função de Gibbs

Relações de Maxwell: Resumo

Exercícios Resolvidos

Exercício Resolvido #1

Lista de Exercícios 06 - Relações de Maxwell - Físico-Química I - UFRGS

O que são as relações de Maxwell da termodinâmica e quais as suas aplicações?

Passo 1

Fala aí! Partiu fazer essa questãozinha teórica pra fortalecer os conhecimentos? Vamos lá!

Bom, o enunciado pediu que a gente diga o que são as relações de Maxwell e suas aplicações… Olha só, vamos relembrar da teoria que vimos, ok?

As relações de Maxwell são um conjunto de equações termodinâmicas que surgem das derivadas parciais mistas dos potenciais termodinâmicos. As aplicações dela são para a gente conseguir calcular propriedades termodinâmicas importantes, que não podem ser obtidas experimentalmente, as principais são: Energia Interna, Entalpia, Função de Gibbs e Função de Helmholtz.

Tranquilinho? Arrasamos!!

Resposta

Passo 1.

Exercício Resolvido #2

Lista de Exercícios 06 - Relações de Maxwell - Físico-Química I - UFRGS

No interior da terra a pressão é provavelmente maior que 3 ⋅ 10 3   k b a r e a temperatura é em torno de 4 ⋅ 10 3 ° C . Calcule a variação na energia livre ao se ir da crosta ao centro da terra num processo no qual Δ V = + 1,0   c m 3 e S = + 2,1   J K   - 1 m o l   - 1 .

Passo 1

Partiu resolver essa questão aí! Bom, a gente precisa encontrar a variação da energia livre de Gibbs da crosta ao centro da terra, ok? Nossos dados são:

Δ V = + 1,0   c m 3   →   1 ⋅ 10   - 6   m 3 S = + 2,1   J K   - 1 m o l   - 1

P = 3 ⋅ 10 3   k b a r → 3 ⋅ 10 6   b a r → 3 ⋅ 10 11   P a T = 4 ⋅ 10 3 ° C

Lembrando lá da equação de Gibbs, temos que:

d G = V d p - S d T

E vamos ter dois momentos, a energia na crosta e no centro da terra, então teremos:

d G 1 = V 1 d p - S 1 d T d G 2 = V 2 d p - S 2 d T

Agora precisamos juntar as duas, ok?

d G 2 - d G 1 = V 2 d p - S 2 d T - V 1 d p - S 1 d T

d G 2 - d G 1 = V 2 - V 1 d p -   S 2 - S 1 d T

Passo 2

Lembrando que:

d G 2 - d G 1 = Δ G V 2 - V 1 = Δ V S 2 - S 1 = Δ S

Então vamos ter que:

Δ G = Δ V d p - Δ S d T

Δ G = Δ V ⋅ Δ p - Δ S ⋅ Δ T

E todas essas variações aí a gente tem! Vamos lá:

Δ G = 1 ⋅ 10   - 6 ⋅ 3 ⋅ 10 11 - 2,1 ⋅ 4 ⋅ 10 3

Δ G = 3 ⋅ 10 5 - 8,4 ⋅ 10 3

Δ G = 291   600   K / m o l

Show de bola!! Encontramos a variação de energia livre!

Resposta

Δ G = 291   600   K / m o l

Exercício Resolvido #3

Relações de Maxwell - Universidade de Coimbra

Suponha que um bloco de metal é comprimido reversível e isotermicamente , à temperatura T , desde um valor de pressão P i até um valor de pressão P f . Quanto calor flui de (ou para) o bloco durante o processo?

Passo 1

E aí? Partiu resolver essa questão juntinhos! Ela parece bem teórica, né? Só tem letra… haha

Mas tá tranquilo que a gente dá conta!

Bom, precisamos saber quanto calor que flui, certo? Então queremos o Q , a equação que define o calor é a seguinte:

Q = T d S

Como estamos variando a pressão, vamos ter uma integral, com os limites nas condições finais e iniciais:

Q = ∫ i f T d S

Mas nosso bloco foi comprimido isotermicamente, né? Isso significa que a temperatura é constante, então:

Q = T   ∫ i f d S

Beleza! Mas quem é esse d S aí? Lembra dele? É a Entropia! E ela é uma função da temperatura e da pressão:

S = S T ,   P

Passo 2

Sendo assim:

d S = ∂ S ∂ T P   d T + ∂ S ∂ P T   d P

Mas lembra que a temperatura não varia? Então d T = 0 , logo:

d S = ∂ S ∂ P T   d P

E nós temos que:

∂ S ∂ P T =   - ∂ V ∂ T P =   - β V

E o d S ficará:

d S =   - β V d P

Então o que flui pelo nosso bloco será:

Q = T   ∫ i f - β V d P

Q =   - β T   ∫ P i P f V d P

Q =   - β ⋅ T ⋅ V ⋅ P f - P i

Opa! Conseguimos! E olha que interessante, nosso calor será negativo, isso significa que o bloco perde calor… Então, o calor flui do bloco!

Resposta

O calor flui do bloco e será:

Q =   - β ⋅ T ⋅ V ⋅ P f - P i

Exercício Resolvido #4

Lista de Exercícios 06 - Relações de Maxwell - Físico-Química I - UFRGS

Demonstre que:

∂ U ∂ P T = V β P - T α

Passo 1

Fala aí! Temos uma questão de demonstração para fazer… Uiii! Relaxa, vai dar tudo certo! Estamos prontos para ela!

Temos que demonstrar que energia interna pode ser representada por essa relação aí… Vamos partir da equação da energia interna:

d U = T d S - P d V

E dividindo pela variação da pressão, com a temperatura constante, vamos ter:

∂ U ∂ P T = T ∂ S ∂ P T - P ∂ V ∂ P T

Agora vamos ver cada termo separadinho… Primeiro a entropia, que será:

∂ S ∂ P T =   - ∂ V ∂ T P =   - α P V

Esse P ali em baixo significa a pressão constante, beleza? Agora vamos para a variação de volume:

∂ V ∂ P T =   - β T V

O T ali em baixo significa a temperatura constante, ok? Show de bola! Agora vamos juntar tudo isso na equação ali de cima, teremos:

∂ U ∂ P T = T - α P V - P - β T V

∂ U ∂ P T =   - T ⋅ α P ⋅ V + P ⋅ β T ⋅ V

∂ U ∂ P T = V β T ⋅ P - α P ⋅ T

Prontinho! Mandamos bem!

Resposta

Passo 1.

Exercício Resolvido #5

Lista de Exercícios 06 - Relações de Maxwell - Físico-Química I - UFRGS

Demonstre que:

d S = C V T d T + ∂ P ∂ T V d V

E também que:

d S = C P T d T - ∂ V ∂ T P d P

Passo 1

Vamos de mais uma demonstraçãozinha? Partiu!!

Bom, na verdade são duas demonstrações análogas, né? Vamos começar pela primeira… Vamos começar lembrando que:

d S = ∂ S ∂ T V d T + ∂ S ∂ V T d V

E lembrando que a equação da energia interna, nos diz que:

d U = T d S - P d V

Podemos dizer que:

d S = d U T + P T d V

E ficaremos com:

d S = 1 T ∂ U ∂ T V d T + ∂ U ∂ V T d V + P T d V

d S = 1 T ∂ U ∂ T V d T + ∂ U ∂ V T + P d V

E lembrando que:

∂ S ∂ T V = C V ∂ S ∂ V T = ∂ U ∂ V T + P

Vamos ficar com:

d S = C V T d T + 1 T ∂ U ∂ V T + P d V

E como:

d A =   - S d T - P d V

∂ S ∂ V T = ∂ P ∂ T V

Vamos ficar, finalmente, com:

d S = C V T d T + ∂ P ∂ T V d V

Show! A primeira demonstração foi feita! Vamos para a segunda!

Passo 2

Agora queremos provar que:

d S = C P T d T - ∂ V ∂ T P d P

Dessa vez vamos por um caminho um pouco diferente, pra vc ver que tem várias formas de provar as relações!

Pra começar, quem é C p ?

C P = ∂ H ∂ T P

Huuum, então na verdade o que a gente quer provar é:

d S = ∂ H ∂ T P T d T - ∂ V ∂ T P d P

Show! A gente pode pegar a relação termodinâmica da entalpia! Parece um bom caminho pra chegar em alguma coisa parecida com essa relação ai!

d H = T d S + V d P

Agora, pra ficar mais parecido ainda, a gente pode dividir todo mundo por d T deixando a pressão constante, igual ao C p !!

∂ H ∂ T P = ∂ S ∂ T P T + ∂ P ∂ T P V

Opaa, derivada de pressão com pressão constante? Podemos zerar isso ai!

∂ H ∂ T P = ∂ S ∂ T P T

Beleza, vamos guardar essa informação um minutinho e vamos pensar na entropia. Sua derivada é uma derivada exata e na relação que queremos provar vemos S como uma função de T e P , certo?

Então podemos escrever a derivada total da entropia!

Só pra a gente refrescar a memória, para escrever a derivada parcial total a gente deriva uma variável, mantendo a outra constante e depois deriva a segunda variável mantendo a primeira constante, nesse caso essas variáveis são T e P , ficamos com:

d S = ∂ S ∂ T P d T + ∂ S ∂ P T d P

Mas: ∂ H ∂ T P = ∂ S ∂ T P T

Substituindo:

d S = ∂ H ∂ T P T d T + ∂ S ∂ P T d P

Huuuum...ta ficando parecido!

Das relações de Maxuell:

∂ S ∂ P T = - ∂ V ∂ T P

Então:

d S = ∂ H ∂ T P T d T - ∂ V ∂ T P d P

Mas lembra que ∂ H ∂ T P é C P ?

d S = C P T d T - ∂ V ∂ T P d P

Show! Arrasamos!

Resposta

Passo 1 e Passo 2.

Exercícios de Livros Relacionados

Duas das quatro relações de Mawell foram deduzidas no texto, mas duas outras não. Complete as deduções, mostrando que ( d S / d V ) T = ( d p / d T ) ve( d T / d p ) s = ( d V / d S ) r .
Use as relações de Maxwell para exprimir as derivadas (a) ( d S / d V ) T e ( d V / d S ) p e (b) ( d p / d S ) v e ( d V / d S ) p em termos do coeficiente de expansão e da compressibilidade isotérmi
O coeficiente de Joule, μ 1 , se define como μ J = ( d T / d V ) U . Mostre que μ J C V = p - a T k T .
Deduza a equação termodinâmica de estado: ( d H d p ) T = V - T ( d V d T ) p Deduza uma expressão de ( d H d p ) T para (a) um gás perfeito e (b) um gás de van der Walls. Neste último caso, estime o
Use as relações de Maxwell para mostrar que a dependência da entropia de um gás perfeito em relação ao volume é da forma S∝ R ln ⁡ V .