Primeira Lei da Termodinâmica
Teoria
A Primeira Lei da Termodinâmica diz o seguinte:
E podemos escrevê-la matematicamente como:
Essa é a primeira Lei da Termodinâmica.
Compreendeu tudo?
Entendeu nada, não é?
hehehehe brincadeirinha, não vamos explicar desse jeito aqui não. Nós somos o Responde Aí, a plataforma de exatas que tem a missão de entregar à você um conteúdo didático, objetivo e claro, bem diferente de como vemos no livro.
Vem comigo entender com calma a primeira lei da termodinâmica.
Variação da Energia Interna de um sistema fechado
Aquela definição formal da primeira lei da termodinâmica que vimos no início dessa página mencionava algo sobre a energia interna de um sistema fechado/isolado, por esse motivo, antes de falar propriamente da primeira lei da termodinâmica precisamos falar sobre a variação da energia interna, beleza?
A energia interna é a energia que o sistema possui a nível molecular e está relacionada com o movimento das moléculas. Essa energia interna varia quando o sistema recebe ou perde calor ou quando o sistema realiza ou sofre um trabalho.
Então, podemos dizer, matematicamente, que a variação de energia interna de um sistema é igual a soma do calor recebido ou cedido pelo sistema com o trabalho realizado ou sofrido pelo sistema:
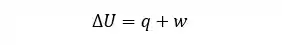
Onde:
é a variação de energia interna; é o calor, e; é o trabalho
Essa fórmula é mega útil, mas temos que entender a convenção de sinais de
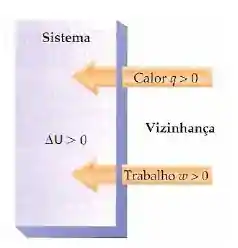
A conveção é a seguinte:
- Trabalho realizado sobre o sistema: POSITIVO, pois energia está sendo fornecida pro sistema, aumentando uma energia interna;
- Trabalho realizado pelo sistema: NEGATIVO, pois energia está sendo cedida pelo sistema, diminuindo sua energia interna;
- Calor cedido ao sistema: POSITIVO, pois o sistema está recendo energia e consequentemente sua energia interna aumenta;
- Calor cedido pelo sistema: NEGATIVO, pois o sistema está gastando energia e sua energia interna está diminuindo.
Primeira Lei da Termodinâmica
Tá, vamos logo para a parte que interessa: O que esse blá blá blá todo tem a ver com a primeira lei da termodinâmica?
TEM TUDO A VER!! A primeira Lei da termidinâmica é uma consequência direta do princípio da conservação de energia, ou seja, ela diz que a energia interna de um sistema fechado/isolado é conservada.
Mas, toma muito cuidado porque isso nem sempre quer dizer que o
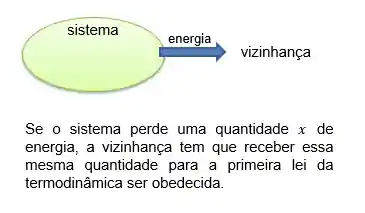
Agora, se estamos falando de um sistema isolado, que não há troca de energia e nem de matéria com a vizinhança, dizer que a energa interna se conserva é dizer que a variação é zero e portanto a energia interna é constante!
Deu pra sacar essa diferença?
Topa fazer um exemplo rapidinho aqui comigo pra ficar mais claro esse conceito?
Exemplo
Um motor de carro pode ser encarado como um sistema fechado. Se esse motor realiza um trabalho de
RESOLUÇÃO:
Vamos aplicar a fórmula da variação de energia:
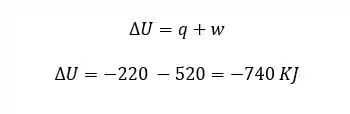
Pela primeira Lei da Termodinâmica, isso significa que a vizinhança desse motor teve uma variação de energia igual a
E é isso! Agora é só praticar com bastante exercícios, que você encontra nessa nossa página aqui: Primeira Lei da Termodinâmica - Exercícios
Se você curtiu esse conteúdo e quer ter acesso completo, assine com a gente!
Primeira Lei da Termodinâmica
Exercícios Resolvidos
Exercício Resolvido #1
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed.Prentice-Hall, 2005, Exercício Como Fazer 5.3
Uma quantidade de ar é expandida e realiza 5,0 kJ de trabalho.
Quanto calor é fornecido ao ar se a energia do ar aumenta em (a) 5,0 kJ, (b) 2,0 kJ, (c) 0 kJ?
Passo 1
Essa questão é bem direto ao ponto: é a aplicação da 1ª lei da termodinâmica todinha.
Se o ar é expandido e realiza trabalho, !
E se a energia aumenta,
Agora vamos analisar as opções:
a)
Passo 2
b)
Passo 3
c)
Resposta
a)
b)
c)
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp280-Exercício 7.5
Uma amostra de gás aquecida em um cilindro consome 524 Kj de energia na forma de calor. Ao mesmo tempo, um pistão comprime o gás e realiza 340 Kj de trabalho. Qual é a variação de energia interna do gás durante o processo?
Passo 1
Pela primeira lei da termodinâmica...
Agora só precisamos decidir os sinais do trabalho e do calor envolvidos no problema!
Se o gás consome o calor, isso quer dizer que ele absorve esse calor e .
Se o pistão comprime o gás, o trabalho é realizado sob o sistema, e também!
Assim, o cálculo da energia interna fica mais tranquilo, só substituir os valores na fórmula!
Resposta
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp280-Exercício 7.13
Em um processo adiabático, não ocorre transferência de energia na forma de calor. Diga se cada uma das declarações seguintes sobre um processo adiabático em um sistema fechado é sempre verdadeira, sempre falsa ou verdadeira sob certas condições (especifique as condições):
a)
b)
c)
d)
e)
Passo 1
Se num processo adiabático não ocorre transferência de energia na forma de calor, podemos definir que
Ou seja,
Logo,
Agora vamos analisar as alternativas:
a) Como se .
Então a alternativa só é verdadeira se .
Passo 2
b) Sempre verdadeiro, já que o processo é adiabático e o sistema é fechado, ou seja, não há nem troca de calor durante o processo, nem troca de calor com as vizinhanças!
Passo 3
c) Sempre falso! Não há troca de calor de nenhum tipo, nem absorção (), nem perda de calor (.
Passo 4
d) Só é verdadeiro se já que e .
Passo 5
e) Sempre verdadeira! , já que e .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp280-Exercício 7.15
Os desenhos abaixo mostram uma visão molecular de um sistema que varia em temperatura constante. Diga, em cada caso, se o calor é absorvido ou perdido pelo sistema, se o trabalho de expansão é executado no sistema ou pelo sistema e prediga os sinais de q e w no processo.
Passo 1
a) Nessa questão temos a transição de fase de sólido para líquido. Se a gente pensa no gelo virando água, por exemplo, sabemos que para que esse processo aconteça, o meio precisa ceder calor para o sólido... Ou seja, o calor nesse caso é absorvido pelo sistema!
Já sobre a expansão, o líquido ocupa menos volume que o sólido: só a gente pensar no espaçamento entre as moléculas ou olhar no desenho que o volume diminui do sólido pro líquido ahahaha
Ou seja, o trabalho vai ser de compressão – realizado sobre o sistema, e, portanto,
Passo 2
b) No B, como o sistema sai da fase vapor para a fase líquida, ele perde calor! Então
Já quanto a expansão, o volume da fase líquida é beeeem menor que o da fase vapor, o que nos leva a concluir que é uma compressão e
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Lista de exercícios UFERSA.
Um gás em um cilindro foi colocado em um aquecedor e ganhou de calor. Se o volume do cilindro aumentou de para contra uma pressão atmosférica de durante o processo, qual é a variação de energia interna do gás no cilindro ?
Passo 1
Nessa questão vamos precisar usar a primeira lei da termodinâmica e a fórmula do trabalho de expansão para um processo isobárico!
Para o trabalho de expansão, podemos calculá-lo como:
Passo 2
Como o gás ganhou calor,
Resposta
Exercício Resolvido #6
Lista de exercícios UFU.
Num dado recipiente contendo um líquido, é imerso um cilindro contendo gás ideal, confinado por um êmbolo móvel, conforme as figuras adiante
O recipiente está sobre uma fonte térmica e a base do recipiente é diatérmica, permitindo trocas de calor entre a fonte e o recipiente. As demais paredes do recipiente são adiabáticas e as paredes do cilindro que contém o gás são diatérmicas. A fonte térmica fornece 2000 J para o sistema formado pelo líquido e o gás, conforme figura (I) acima. Devido ao calor fornecido pela fonte térmica, a temperatura do líquido aumenta de 3K, consumindo 1500 J. Por outro lado, o gás realiza uma expansão com um aumento de volume de , a uma pressão constante de , como representado na figura (II) acima.
a) Calcule o trabalho realizado pelo gás.
b) Calcule a variação da energia interna do gás.
c) Nesse processo, o que acontece com a energia cinética das partículas que compõem o gás: aumenta, diminui ou não muda? Justifique a sua resposta.
Passo 1
a) O trabalho à pressão constante é calculado pela fórmula:
Passo 2
b) A energia interna do gás pode ser calculada pela 1ª lei da termodinâmica:
Como o calor cedido pela fonte é de 2000J e 1500J é absorvido pelo líquido, podemos concluir que 500J são absorvidos pelo gás!
Como o calor é absorvido, .
Passo 3
c) Como a energia interna aumenta, a temperatura aumenta e, consequentemente, a cinética das partículas também aumenta!
Se a variação de energia interna fosse negativa, a temperatura diminuiria e a velocidade das partículas também.
Resposta
a) -400J
b) 100J
c) A cinética das partículas aumenta!
Exercício Resolvido #7
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed.Prentice-Hall, 2005, Exercício 5.23
Um gás é confinado em um cilindro equipado com um pistão e um aquecedor elétrico, como mostrado na ilustração desse exercício. Suponha que se forneça corrente para o aquecedor de tal forma que sejam adicionados 100J de energia. Considere duas situações diferentes. No caso (1) é permitido que o pistão se mova à medida que a energia é adicionada. No caso (2) o pistão está fixo, de tal forma que não se possa mover.
a) Em qual caso o gás tem a maior temperatura depois da adição da energia elétrica?
b) O que você pode dizer sobre os valores de q e w em cada um desses casos?
c) O que você pode dizer sobre os valores relativos de para o sistema (o gás no cilindro) nos dois casos?
Passo 1
a) A temperatura está diretamente ligada à energia interna. Quanto maior a variação da energia interna, maior a temperatura!
No caso 1, como o pistão pode se mover, o gás pode realizar trabalho! Quando o gás realiza trabalho, ele diminui a variação de energia interna, diminuindo assim o aumento de temperatura!
Por isso, a temperatura vai ser maior no caso 2.
Passo 2
b) Como o calor é cedido pelo aquecedor elétrico ao sistema, .
Quanto ao trabalho, no caso 1 ele é negativo, já que é o ar que realiza o trabalho. (
No caso 2, como o pistão não pode se mover, não há variação de volume, e o trabalho vai ser 0! (
Passo 3
c) Como no caso 2, e é certo que , já que, pela primeira lei da termodinâmica,
Já no caso 1, o valor de vai depender dos valores de e de , já que eles tem sinais opostos.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed.Prentice-Hall, 2005, Exercício 5.25
a) Qual o significado do termo função de estado?
b) Dê um exemplo de grandeza que é função de estado e de uma que não é.
c) A temperatura é função de estado? Justifique sua resposta.
Passo 1
a) Uma função de estado é uma função que só depende dos valores iniciais e finais, e não do caminho que foi pego para chegar à esse valor.
Passo 2
b) A energia interna é uma função de estado, já que ela só depende da energia interna final e inicial do sistema, e não do caminho que foi pego para chegar na energia interna final.
Já o trabalho não é uma função de estado, já que o processo que produziu aquele trabalho é importante na hora de calcularmos o trabalho. Se ele fosse uma função de estado, poderíamos simplesmente calcular o de trabalho”.
Passo 3
c) A temperatura é uma função de estado, pois se temos uma temperatura final e inicial, pouco importa para o cálculo desse como conseguimos mudar essa temperatura!
Resposta
Ei, a resposta está no passo a passo :)