Terceira Lei da Termodinâmica
Produzido por Juliana EcheniqueTeoria
A terceira lei da termodinâmica diz que: “A variação da entropia de qualquer transformação física ou química tende a zero quando a temperatura tende a zero, admitindo-se que todas as substâncias envolvidas estão perfeitamente ordenadas.”
📢 Clique pra ver mais:
- Terceira Lei da Termodinâmica: Exercícios Resolvidos
- Introdução à termodinâmica
- Primeira lei da termodinâmica
Mas e na prática, o que isso significa?!
Pela terceira lei da termodinâmica se a temperatura tende a
Ou seja, a variação da entalpia é zero quando a temperatura tende a zero absoluto.
Terceira Lei da Termodinâmica e a Vibração dos Sólidos
Na figura abaixo temos um sólido puro. Na esquerda, ele está quente, então suas moléculas estão vibrando bastante. Já na direita, o sólido foi resfriado, estão suas moléculas estão vibrando menos.
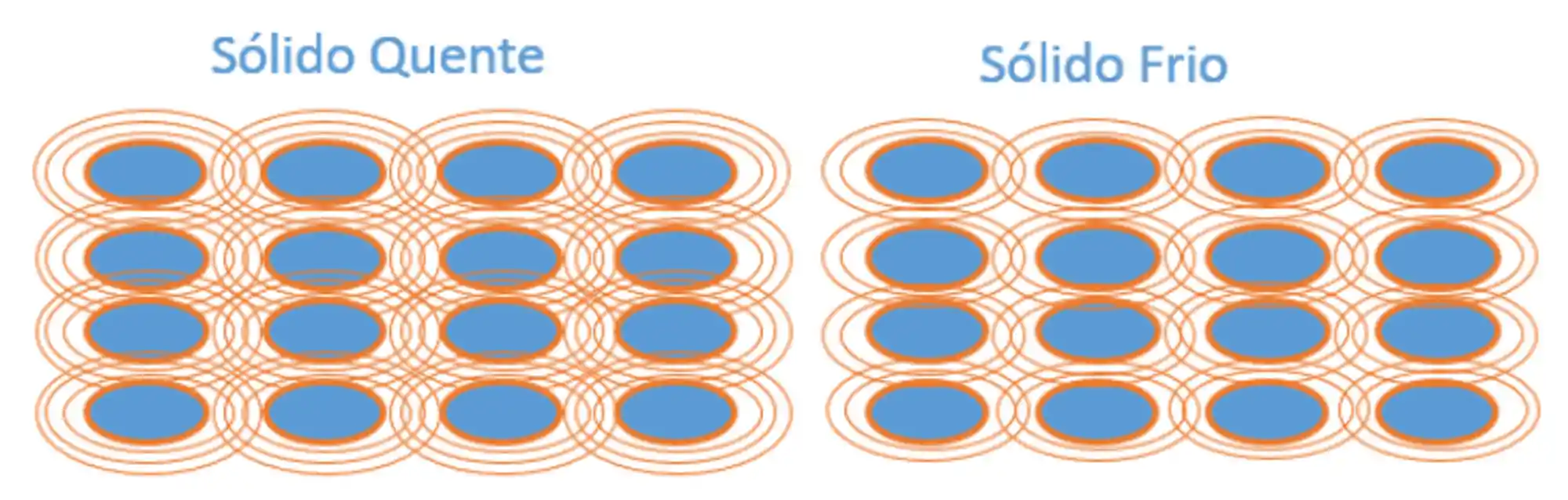
Em alta temperatura, com maior vibração, o grau de desordem do sistema é maior, então a entropia é maior. Em média, as moléculas têm maior agitação no corpo quente. Mas essa agitação aí é a agitação média. Na verdade, ela não está homogeneamente distribuída pelas moléculas. Então a gente vai ter umas moléculas que vibram muuuito, enquanto outras vibram menos.
Essa diferença no grau de agitação das moléculas também contribui para o fato de que em sólidos quentes o grau de desordem do sistema seja maior. Quanto maior a temperatura, maior a diferença de vibração entre a molécula menos agitada do corpo e a mais agitada.
Entalpia no Zero Absoluto
Agora vamo supor que o corpo é resfriado até o
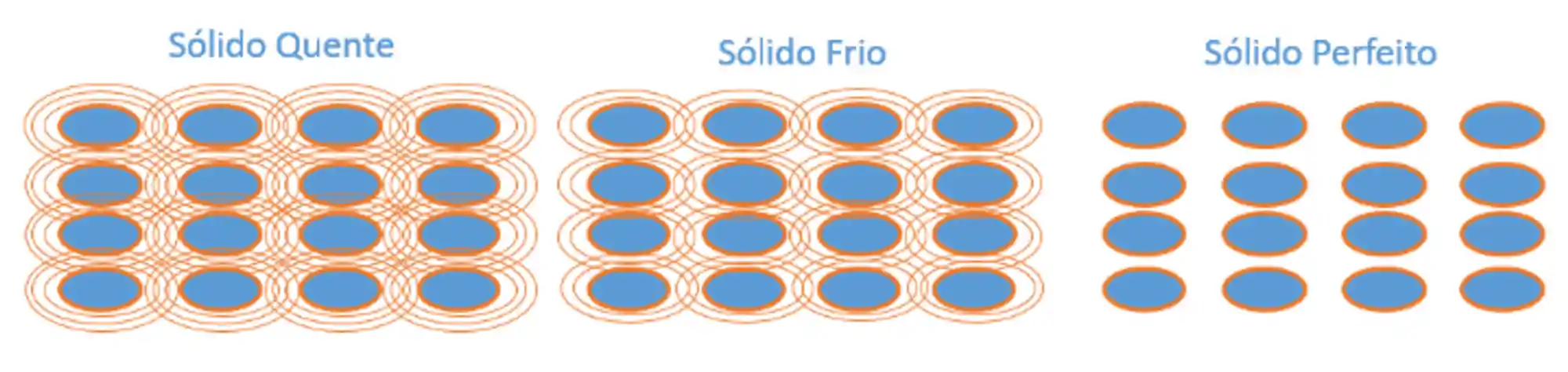
A energia vibracional do sólido perfeito está distribuída de forma homogênea, já que não há nenhuma energia para se distribuir. Por isso a sua entropia será nula.
E aí você entendeu a terceira lei! No zero absoluto não tem vibração, o corpo, ou o sistema, ou o universo, apresenta um único microestado de energia possível, então a entropia é nula.
Uma consequência direta dessa lei é que é impossível atingir o 0zero absoluto, não importa o quão bem planejado e executado o processo seja e nem o número de operações que se execute. Outra consequência dessa lei é que tratamos a entropia como sendo uma função da temperatura e que tem o seu valor mínimo no zero absoluto!
Agora vamos praticar com exercícios?
Terceira Lei da Termodinâmica e a Vibração dos Sólidos
Entalpia no Zero Absoluto
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado de James E. Brady e Gerard E. Humiston Volume 1, 2ª edição: Livros Técnico Científicos Editora.
A entropia de mistura estando a 0 K teria o valor igual a zero?
Passo 1
Uma mistura apresenta diferentes moléculas e com isso há várias possibilidades de distribuição das moléculas nesse sistema. Para a gente ver melhor isso dá uma olhada nesse exemplo aqui de uma mistura que tem apenas uma molécula diferente.
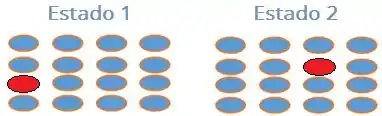
Observe que há um novo estado possivel para o sistema em função da posição relativa das moléculas.
Então, para misturas resfriadas até o zero absoluto, a entropia depende da quantidade de combinações das posições relativas das moléculas. Daí o calculo da entropia que é dado pela fórmula:
Onde:
é a constante de Boltzmann
é a quantidade de microestados equivalentes
Vai resultar a um valor constante pois há um número limitado de combinações das posições das diferentes moléculas que compõem o sistema. Contudo, essa constante tem um valor não nulo, visto que há mais de uma possibilidade de distribuição das moléculas nessa mistura e portanto:
O que implica que:
Vale lembrar que cada mistura terá um valor diferente para a sua entropia no zero absoluto.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Hipoteticamente uma mistura está em uma temperatura muito próxima ao 0 K. Determine se é possivel separar a mistura através de um processo adiabático obter as substâncias puras equivalentes a mesma temperatura.
Passo 1
Sabemos que quando uma substância pura está no zero absoluto tem entropia nula, equanto que as misturas possuem uma entropia maior que zero. Então sendo assim a variação da entropia nesse caso sera dado por:
Considerando que a entropia para substâncias puras a é nula temos que:
Aí temos então que esse processo apresenta uma variação de entropia negativa
Passo 2
Ao se tratar de uma transformação adiabática temos que a dessa transformação é nula e aplicando o calculo da energia livre de Gibbs teremos se esse processo é espontâneo ou não.
Considerando que estamos a uma teperatura , ente que Que aplicando os valores teremos:
De forma que o valor de o que comprova que esse processo não é espontâneo, portanto essa separação não é possivel de forma adiabática.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Adaptado da lista de Exercícios do professor Folmer UFRJ
Considere a fórmula a seguir para o cálculo da entropia
Embora saibamos , não podemos usá-lá para calcular a entropia absoluta de um gás ideal a uma dada temperatura (assumindo que não há mudança de fase entre ). Explique por que isso ocorre.
Passo 1
A resolução daquela integral é bem simples.
Primeiro a gente tem que ver que o de um gás ideal não varia em relação à T. Então ele sai tranquilão pra fora da integral:
Em seguida tem que lembrar que a integral de é o .
Que fica:
E aí, já sacou qual é o problema?
Bem o problema é que não existe!! É uma indeterminação, então não tem como calcular essa entropia.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
Um processo usando os gases hidrogênio e oxigênio foi idealizado em duas etapas da seguinte forma:
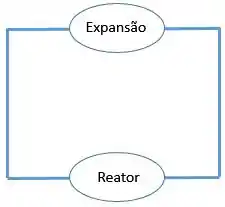
Na primeira etapa ocorre a expansão adiabática, onde os gases sofrem uma reação reversível havendo a produção de trabalho para movimentar um motor.
Considere a ocorrência da seguinte reação:
A segunda etapa ocorre no reator, onde os gases reagem formando um produto de maior entalpia num processo endotérmico, isovolumétrico e reversível.
Indique a reação que ocorre no reator. Sabendo que os módulos das energias envolvidas das duas etapas são iguais, verifique se este processo respeita cada uma das leis da termodinâmica. Considere que o processo acontece a temperatura constante de .
Passo 1
No reator a única possibilidade que é plausível é a ocorrência da reação de decomposição da água.
Temos aqui uma reação endotérmica, que ocorre com absorção de calor do meio externo.
Passo 2
Nesse processo ocorre realização de trabalho numa câmara após uma reação em que os gases reagiram formando um produto de menor volume, afinal háverá menor quantidade de gases, a expansão de gases aqui pode ocorrer já que a reação é exotérmica. Analisando a variação de energia interna do gás temos a seguinte equação:
Daí vemos que a energia interna do gás varia para um estado de menor energia.
Passo 3
O reator permite a reação de formação de água
A variação de energia interna do gás nessa etapa será igual ao , pois o processo é isovolumétrico, logo não há trabalho sendo realizado.
O processo como um todo tem uma variação da energia interna do gás ao longo das duas etapas do processo nulo, pois segundo o enunciado as energias das duas etapas são simétricas.
Dessa forma o processo consegue respeitar a primeira lei da termodinâmica.
Passo 4
Quanto a segunda lei da termodinâmica, têm-se um processo em que há absorção de energia térmica no reator e posteriormente a energia é liberada na forma de trabalho por meio da expansão isotérmica dos gases após a formação da água. Isso desrespeita a segunda Lei da termodinâmica pois como o processo é isotérmico, todo a energia liberada pela reação química está sendo transformada em trabalho de expansão.
Vale lembrar que embora a primeira lei demonstre a conservação de energia, a segunda estabelece que o calor não pode ser convertido integralmente em trabalho.
Passo 5
A terceira lei institui que variação de entropia em processos no tenham uma variação de entropia nula, essa lei institui também que essa temperatura é inalcançável então só do processo ser idealizado nessa situação o processo já desrespeita claramente a terceira lei.
Resposta
Temos a seguinte reação
Sobre a validade do processo frente as Leis da termodinâmica:
O processo respeita a 1ª Lei da Termodinâmica.