A coluna de destilação que fará a separação de uma mistura de benzeno e tolueno com de massa de tolueno operará a . O produto de topo deve conter em massa de benzeno, o produto de fundo em massa de tolueno e a razão de refluxo externa de topo será de . A carga e o refluxo no topo são vapores saturados e deverá entrar no seu prato ótimo com uma vazão de . Determine:
- As vazões dos produtos de topo e de fundo.
- O número de estágios de equilíbrio necessários.
- O prato ótimo de carga.
- A razão de refluxo mínima.
- O número de estágios na razão de refluxo total.
Dados de Equilíbrio do Sistema Benzeno – Tolueno a
![]()
Passo 1
Para começar a questão , precisamos fazer o balanço de massa para calcular o produto de topo e de fundo. O balanço global fica:
E o balanço por componente:
Substituindo em termos de concentração de benzeno, temos que:
E então, encontramos que:
Passo 2
No entanto, nós vimos que para aplicar o método Mc-Cabe Thiele, as vazões precisam estar em molar e não em massa. Logo, vamos precisar da massa molar do benzeno e da massa molar do tolueno para fazer essas conversões.
Como sabemos que tanto quanto possuem benzeno e tolueno, podemos escrever a seguinte equação para converter as unidades.
Substituindo para os dois temos que:
As frações que temos são mássicas, também precisamos calcular as frações molares para poder utilizar.
Com isso respondemos a letra a), que pede as vazões do produto de topo e de fundo, só que em vazão e fração molar.
Podemos também fazer a mesma coisa para a nossa carga, que possui de tolueno, ou seja, de benzeno em massa.
E a fração molar de benzeno na carga pode ser calculada por:
A partir de agora, podemos começar de verdade a parte de destilação e Mc-Cabe Thiele.

Passo 3
O próximo item que precisamos responder é o número de estágios de equilíbrio necessários. Para responder isso, vamos precisar de montar o gráfico com a tabela que a questão forneceu para gente, pois conseguiremos aplicar o método Mc-Cabe Thiele. Lembrando de também fazer a linha da diagonal, que é a nossa linha azul.

Agora, vamos marcar os produtos de topo e de fundo, além da carga e a reta q. Lembrando que o produto de topo e a carga são vapores saturados, então a reta q vai ser horizontal e o condensador será total 😊
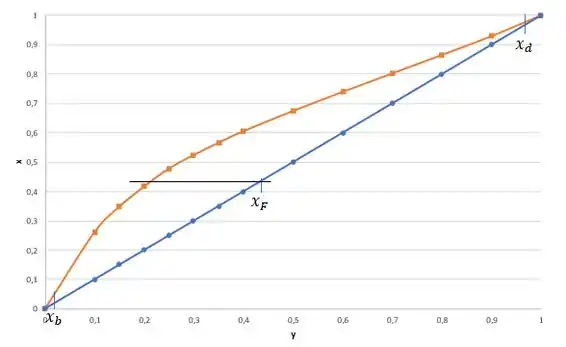
A Razão de Refluxo externa é , de acordo com o enunciado. Com isso, podemos calcular a interseção da seção de operação com o eixo .
Com isso, conseguimos marcar a reta de operação da seção de absorção e esgotamento e traçar o número de estágios. Nesse caso, temos 23 estágios.
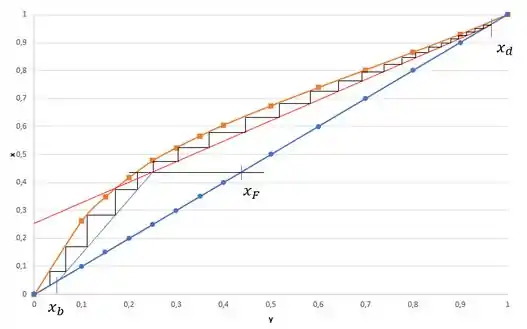
Passo 4
Na letra c, precisamos determinar o prato ótimo de carga. O prato ótimo de carga é aquele que a reta de carga corta os estágios traçados. Nesse caso, olhando pelo gráfico é 19º estágio.
Passo 5
A letra d) pede a Razão de Refluxo Mínima é aquela que encontramos quando forçamos o “pinch” na reta de carga.
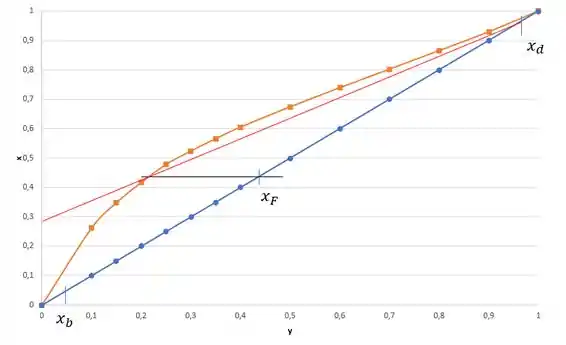
Pelo “Pinch”, vemos que a interseção no eixo y é . Logo a razão de refluxo mínima pode ser calculada pela fórmula da interseção.
Portanto, .
Passo 6
A letra e) pede para a gente calcular o número de estágios na Razão de Refluxo total. Nesse caso, precisaremos traçar os estágios sem considerar as retas de operação. Podemos representar da seguinte forma:

Nessa condição, temos 11 estágios.
Portanto, concluimos a questão 😊
Resposta
- As vazões dos produtos de topo e de fundo.
- 23 Estágios
- 19º Estágio
- 11 estágios.