Faça uma função recursiva que receba um inteiro positivo n e imprima a soma dos dígitos de n. Ex: n=215 → 8, n=45 → 9
Passo 1
Fala aí, maninho! Tudo na paz? Se liga, nessa questão o professor quer que a gente some todos os dígitos de um número inteiro usando recursão.

Bora segurar as lágrimas e tentar fazer a questão. Se liga, o que a nossa função precisa saber de dado externo pra funcionar?! Bom… Ela precisa saber qual o número que a gente quer somar os dígitos e só! Então esse vai ser nosso único parâmetro.
E se liga que você pode dar o nome que você quiser pra função e pro parâmetro. Siga seu coraçãozinho! Mas é uma boa ideia dar nomes intuitivos, ok? Usar o nome “n” não é legal, mas eu sou rebelde.

Mentira! Eu escolho nomes pequenos aqui só pra não gastar muito espaço na tela, caso você esteja lendo pelo seu celular… Mas enfim, bora começar a escrever nossa função!
Passo 2
Bom, pra resolver recursivamente a gente precisa fazer o problema grande virar o mesmo problema, só que menor… Como fazer isso nesse caso?! Hmmmmm.

Vamos pensar no número 215, que o professor passou de exemplo no enunciado. Tu percebe que o somatório desse número é um dígito + o somatório do resto?
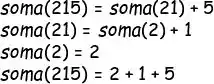
Obs: na teoria, não faz diferença se a gente for separando o último dígito ou o primeiro dígito.
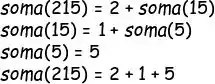
Mas na prática faz, porque a gente não sabe separar, de forma matemática. o primeiro dígito do resto. Mas a gente sabe separar o último, usando divisões por 10. Olha nesse exemplo como a gente pode fazer pra separar o último dígito de um número:
![]()
Show! Mas vamos dar só mais uma olhada em qual vai ser nosso caso base. Percebeu que na ilustração a gente parou de subdividir o problema quando o número só tinha um dígito? Ou seja, quando o número é menor que 10 a gente pode parar. Esse é o nosso caso base. Mas não é a única forma! Dá uma olhada:
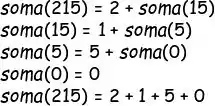
Olha! A gente também consegue fazer n == 0 como um caso base. Problemas de programação sempre têm mais de uma resposta, e eu tô querendo enfatizar que se você fizer diferente não tá errado, ok? Nessa resolução, vou escolher usar o caso base como n

Passo 3
Agora a gente já pensou em qual vai ser o caso base e em como subdividir o problema do enunciado. A gente só precisa escrever essa lógica no corpo da nossa função, em Python.

Pronto! Se for menor que 10 a gente retorna o próprio n, e se for maior a gente retorna a soma do último com o somatório do resto dos dígitos. Vamo só fazer um teste pra ver se a função tá funcionando de boas...
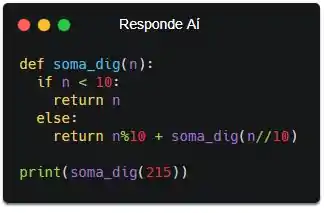
A gente espera que o resultado desse programa seja 8, e quando a gente executa:
![]()
O resultado foi 8 mesmo! EBAAA

Mas antes de finalizar o exercício, vou te falar sobre umas coisas… Se você estiver sem tempo, pode pular pra próxima questão!
Passo 4
Cara, vou copiar e colar aqui a ideia usando n == 0 como caso base.
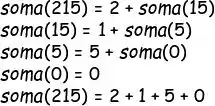
O resultado no fim vai ser exatamente o mesmo, mas pode ser que você prefira fazer dessa forma (eu, geralmente, prefiro). Então eu vou adaptar a última resposta pra usar esse caso base pra você ver como ficaria, ok? Olha:
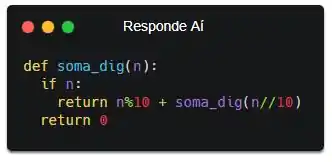
Se liga que o if tá invertido também. O que tá acontecendo é: “se n for diferente de 0, retornar o último dígito + a soma dos outros. Caso contrário, retornar 0”. E é exatamente isso que a gente fez ali em cima nas continhas! Outra coisa que queria falar sobre é que a gente omitiu o else dessa vez. Cadê o else??

Então… Lembra que quando a gente tava falando de funções, eu comentei que a função acaba quando chegamos em um return?! A ideia nesse programa é que se o primeiro if for verdadeiro, a função vai chamar o return e vai chegar ao fim. O segundo return só vai ser executado se o if for falso. Reparou que, nesse caso, o else se tornou desnecessário?!

Se você tivesse colocado também não teria problema, mas eu queria comentar em algum lugar que nem sempre você precisa do else. Quando o primeiro if tem o return dentro, o else se torna desnecessário! Mas isso é só pra complementar seu conhecimento, ok? Na dúvida, coloca o else lá!

Valeuuuuuu!
Resposta
