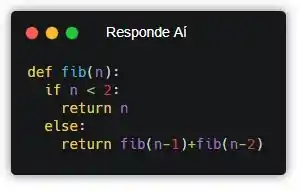
Faça uma função recursiva que receba um número inteiro positivo n e imprima o n-ésimo número da sequência de Fibonacci. Ex: n=5 → 5, n=2 → 1
Passo 1
Coe, truta! Muita coletividade na quebrada! Dinheiro no bolso, sem miséria… É nós!

A primeira coisa que a gente tem que fazer pra resolver essa questão é… saber o que é sequência de Fibonacci. Segundo o Wikipédia, é uma sequência que começa com 0 e 1 e depois vai sendo a soma dos últimos dois números. Tipo assim:
![]()
E assim vai! Parece que a gente tem que criar uma função recursiva que recebe como parâmetro um número inteiro e retorna o número correspondente na sequência… E, pela definição, a gente já saca que a sequência é naturalmente recursiva. Se liga só:
![]()
Vamos começar escrevendo o cabeçalho da função!
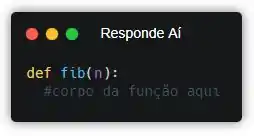
Pronto! Agora, a gente precisa pensar no caso base…
Passo 2
Bora começar vendo o caso que a função termina. Bom, se for 0 ou 1 a gente já sabe a resposta. Olha os números dos itens…
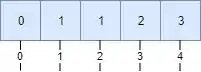
Se liga que o n dá um índice e a gente tem que retornar o número da sequência, heinn! Não confunde! E repara, mano, que os índices e os números da sequência são iguais nos dois primeiros itens. Esses dois itens também são, coincidentemente, nossos casos base. Quando queremos fibonacci de 0, podemos retornar 0. Mesma coisa com o 1, retornamos 1. Vamos escrever em Python!
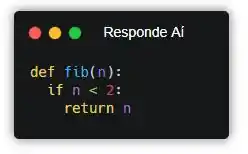
Pronto! Se for menor que 2 (0 ou 1), a gente retorna o próprio valor… Mas se for maior a gente precisa retornar a sequência.
Passo 3
Pra gente retornar o valor da sequência caso seja maior que n, bora dar uma segunda olhada na definição de fibonacci…
![]()
Olha, a gente pode retornar de boas igualzinho na definição da sequência.
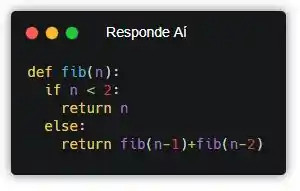
E pronto! Só falta a gente testar!!

Passo 4
Pra testar, eu vou rodar o programa com alguns prints e vou testar com os dados que o professor passou no enunciado pra ver se bate.
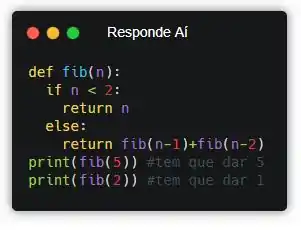
Ala! Depois de executar, deu certinho!
![]()
O resultado foi exatamente como no enunciado! hihihi Finalizamos por hoje, capitão! Te vejo na próxima jornada (chamada exercício de fixação)!

Resposta