Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Redução de Grau – Briot-Ruffini

Ver Teoria
Exercício 123456

Enunciado

Uma das raízes do polinômio 2 x 3 + x 2 - 7 x - 6 é 2. Pode-se afirmar que:

  1. As outras raízes não são reais.
  2. As outras raízes são 17 e -19
  3. As outras raízes são iguais
  4. As outras raízes estão entre -2 e 0

Passo 1

Temos que o polinômio será sempre divisível pelas suas raízes sem resto. Vamos fazer isso para simplificá-lo. Usamos Briot-Ruffini, chegamos ao quadro:

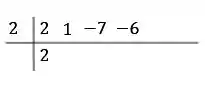
Completando-o:

2 ⋅ 2 + 1 = 5

5 ⋅ 2 - 7 = 3

3 ⋅ 2 - 6 = 0

Veja que o resto é zero conforme esperado. Podemos reescrever esse polinômio na forma: P x = 2 x 2 + 5 x + 3 x - 2

Passo 2

As raízes do polinômio de segundo são as que faltam. Ele é mais fácil de resolver, podemos usar Bhaskara: 2 x 2 + 5 x + 3 = 0

x 1,2 = - b ± b 2 - 4 a c 2 a = - 5 ± 25 - 4 2 3 2 2 = - 5 ± 25 - 24 4 = - 5 ± 1 4

Assim, as raízes serão:

x 1 = - 6 4 = - 3 2

E: x 2 = - 4 4 = - 1

Passo 3

Vamos ver qual alternativa se encaixa no resultado encontrado. Vemos que as raízes são reais, então a letra (a) está fora. Também não são nem 17 e - 19 , então a (b) já era também. As raízes não são iguais, tiro fatal na (c).

Temos que - 3 / 2 = - 1.5 . Junto de - 1 , vemos que as raízes estão entre - 2 e 0 , logo a alternativa correta é a letra (d).

Resposta

Letra d.