4. Sejam e números reais e considere o polinômio . Ao dividir por , o resto é e ao, dividir por , o resto é . Então o valor de é
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos a seguinte função,
E queremos saber quanto vale . Para isso, vamos usar as informações sobre as divisões e o resto de cada divisão e para fazer essa conta vamos usar o dispositivo de Briot-Ruffini.
Bora lá!
Passo 2
A primeira divisão que temos é por , com resto . Aplicando Briot-Ruffini, ficamos com
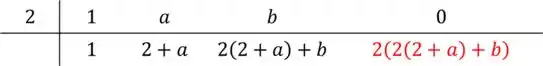
O nosso resto é e o enunciado disse que resto é . Fazendo essa igualdade
Repara que temos duas icognitas e uma equação! Então precisamos encontrar mais uma relação com as informações dadas.
Passo 3
Agora vamos para a nossa próxima divisão! Temos que ao dividir por , o resto é . Aplicando Briot-Ruffini:
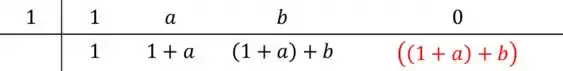
O nosso resto é e o enunciado disse que resto é . Fazendo essa igualdade
Opaaa! Temos uma segunda equação, podemos montar o nosso sistema!
Passo 4
Ficamos assim,
Isolando
Substituindo na primeira equação do sitema,
Prontinho!