Qual o valor de que faz com que o resto da divisão de por seja ?
Passo 1
Vamos usar Briot-Ruffini para resolver essa questão. Queremos:
O denominador zera em . Vamos adicionar isso ao quadro:

Agora, marcamos os coeficientes na parte superior direita, lembrando que tem que entrar:
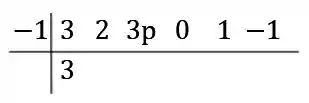
Passo 2
Agora, vamos multiplicar o primeiro coeficiente na parte inferior direita pelo na parte superior esquerda:
Somamos isso ao segundo coeficiente para parte superior direita:
Ficando:
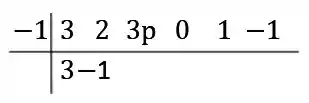
Fazendo agora aos demais:
Agora:
E:
Por fim:
Passo 3
Esse último resultado é justamente o resto, pois é o valor mais à direita no quadro do Briot-Ruffini. Queremos que esse resto seja , então igualamos:
Passo 4
Se utilizássemos o Teorema do Resto, teríamos que o resto da divisão de por , ou seja, por é igual a .
Vamos calcular dessa forma?
Como queremos que o resto seja igual a :