Uma mistura aquosa de etanol com 60% de água a 60 °C e 1 atm é aquecida. Informe qual é a temperatura quando 80% da amostra for vaporizado.
Sabendo que seu diagrama é dado por:
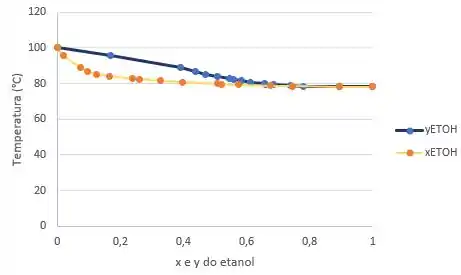
Passo 1
Precisamos achar a temperatura quando temos 80% vaporizado, que é a mesma coisa que dizer que temos 20% líquido. Então, podemos partir da fórmula que chegamos no exercício anterior para definirmos a fração de líquido.
O nosso não mudou, já que a carga também não foi alterada. Então:
Podemos trabalhar com essa equação até obter:
Passo 2
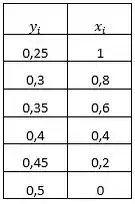
Então, vamos avaliar quais pares , em que cada um deles varie entre 0 e 1, podem ser utilizados.
Para facilitar e não termos que ficar chutando várias hipóteses, vamos isolar o , então vemos que:
Como , podemos fazer o seguinte:
Logo, temos os valores para os quais vamos avaliar a variação de .
Nesse caso, iremos procurar no gráfico os seguintes pontos para ver a temperatura e localização de cada um.
Vamos verificar o primeiro ponto ().
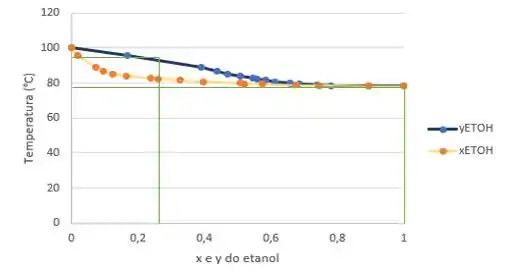
Repara que olhando esses pontos no gráfico, eles não estão na mesma altura. Dessa forma, não podem ser esses os pontos, pois cada um se refere a uma temperatura diferente (só olhar o eixo vertical).

Devemos fazer essa análise para todos os pontos possíveis, até chegar em pontos de que indiquem a mesma temperatura.
Passo 3
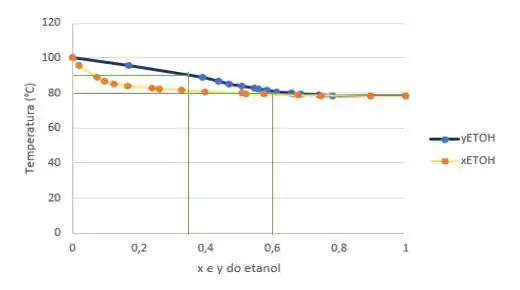
Para o segundo ponto ( e ), as temperaturas indicadas também não são as mesmas. Então, esse ponto também não serve.
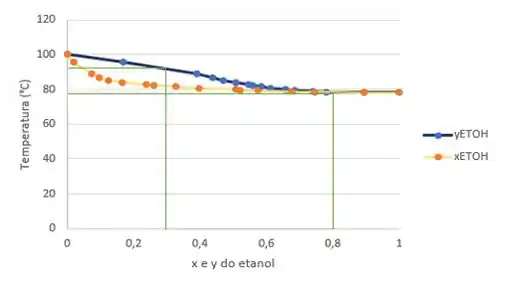
Passo 4
Para o terceiro ponto ( e ), as temperaturas indicadas também não são as mesmas. Então, esse ponto também não serve.
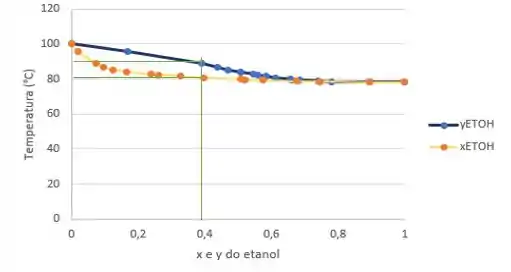
Passo 5
Para o próximo ponto ( e ), também não é a mesma temperatura.
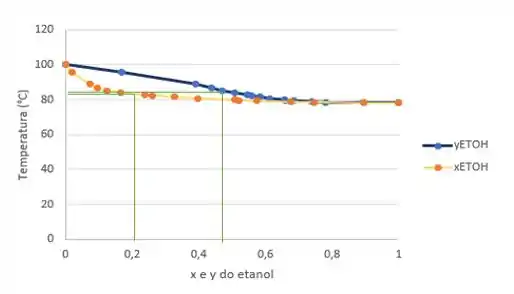
Passo 6
Para o próximo ponto ( e ), as retas ficam quase na mesma temperatura, então, esse é o ponto que fica mais próximo do equilíbrio entre . E a temperatura fica próxima a 85 °C. Portanto, essa é a temperatura que vamos utilizar para responder a questão.
Resposta
Temperatura próxima a 85°C.