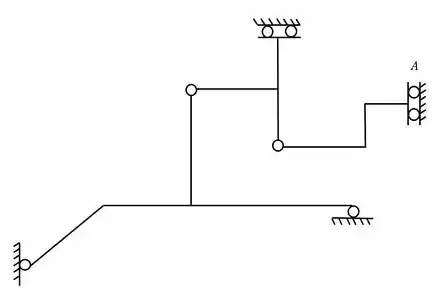
Determine qual o melhor apoio a ser colocado no ponto A da grelha abaixo.
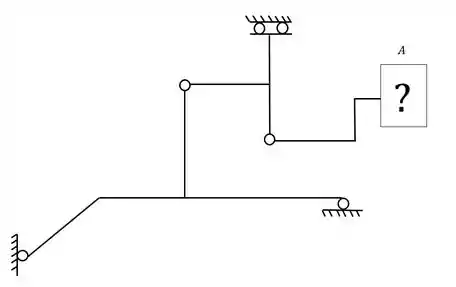
Passo 1
Antes de qualquer coisa temos que relembrar o nosso passo a passo para resolver esse tipo de problema. Para isso temos que respeitar algumas regrinhas, que são
- Achar todas as rótulas e dobradiças, pois serão possíveis pontos de quebra para analisarmos grelhas simples
- Quebrar essas rótulas e dobradiças e substituir por apoios fictícios
- Analisar se as treliças formadas são simples e isostáticas
- Definir o melhor apoio para estrutura (alguns professores deixam um apoio faltando e pedem para o aluno dizer qual seria o melhor apoio para aquela estrutura)
- Pegar todas as reações de apoios fictícios e transferir para as barras em que eles se apoiam
- Definir uma ordem de solução
- Calcular as reações de apoio
- Calcular os diagramas
Vale lembrar que o nosso problema não usará todo esse passo a passo, mas teremos questões mais complexas em que teremos que usar completamente o passo a passo dado acima.
Dito isso tudo, vamos aplicar nosso passo a passo na grelha do nosso problema.
Passo 2
Como vimos primeiro devemos achar as possíveis rótulas a serem rompidas, e no nosso exemplo só temos duas possíveis rótulas a serem rompidas, que marcamos aqui em baixo.
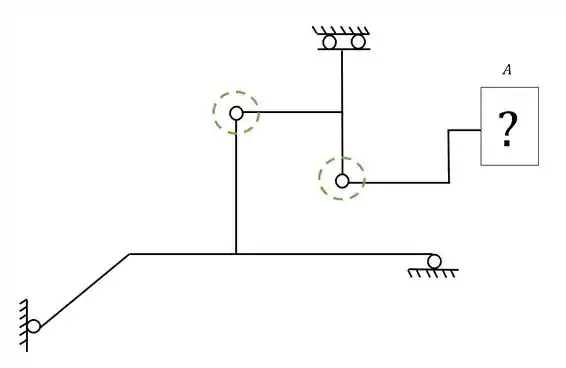
se lembrarmos o que vimos na aula teórica, lembraremos que o rompimento de rótulas gera apoios do primeiro gênero, e o rompimento de dobradiças, geram também, dobradiças.
Porém, vamos ao próximo passo então.
Passo 3
O segundo passo consiste em olharmos a nossa estrutura separada e com o apoio fictício, mas onde podemos romper?
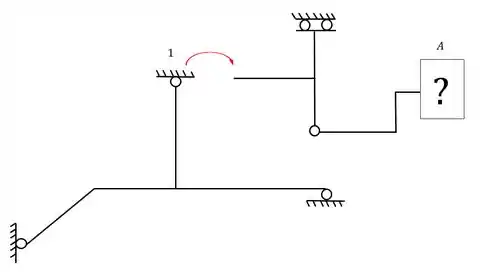
Agora pode surgir a dúvida se rompemos a rótula 1 ou 2. Vamos romper as duas, uma de cada vez, e ver no que dá.
- Rompendo a Rótula 1
- Rompendo a Rótula 2
Perceba que ao romper a rótula 1 teremos a seguinte estrutura
Fazendo o balanceamento de equações e incógnitas da primeira estrutura veremos que ela possui 3 apoios do primeiro gênero, logo, possui 3 incógnitas, já que cada apoio gera uma incógnita. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.
Já a segunda estrutura nós vemos que possui 1 dobradiça que nos dá 2 incógnitas e 1 rótula com 2 barras que nos da 1 equação. Dessa forma temos ao todo 4 equações, 3 de equilíbrio e 1 da rótula, e 2 incógnitas, ou seja, o melhor apoio, nesse caso a ser colocado no ponto A é uma dobradiça que nos dará mais 2 incógnitas, fechando um total de 4 incógnitas e 4 equações
Perceba que ao romper a rótula 2 teremos a seguinte estrutura
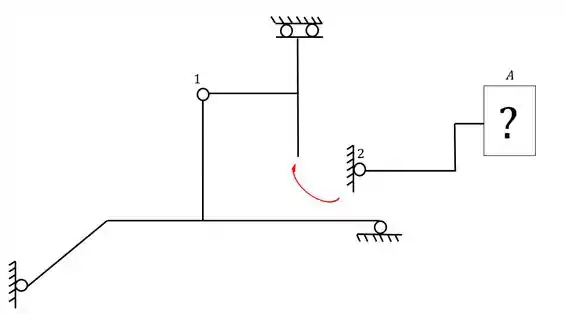
Fazendo o balanceamento de equações e incógnitas da primeira estrutura veremos que ela possui 2 apoios do primeiro gênero e 1 dobradiça, logo, possui 4 incógnitas, já que cada apoio do primeiro gera uma incógnita e a dobradiça gera 2, vale lembrar também que a rótula irá gerar mais 1 equação. Como temos 4 incógnitas e 4 equações, sabemos que a nossa estrutura foi dividida corretamente.
Já a segunda estrutura nós vemos que possui 1 apoio do primeiro genero que nos dá 1 incógnita. Dessa forma temos ao todo 3 equações, sendo as 3 de equilíbrio, e 1 incógnita, ou seja, o melhor apoio, nesse caso a ser colocado no ponto A é uma dobradiça também que nos dará mais 2 incógnitas, fechando um total de 3 incógnitas e 3 equações.
Ou seja, independente da rótula que quebrássemos, usaríamos como apoio do ponto A uma dobradiça.
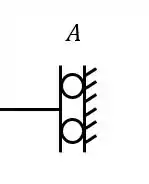
Resposta
O apoio a ser usado no ponto A é uma dobradiça