Determine as reações dos apoios A e B da grelha abaixo
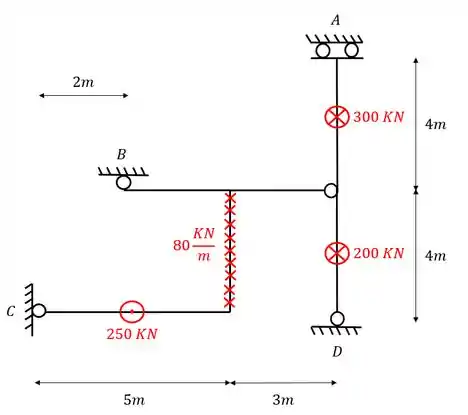
Passo 1
Antes de qualquer coisa temos que relembrar o nosso passo a passo para resolver esse tipo de problema. Para isso temos que respeitar algumas regrinhas, que são
- Achar todas as rótulas e dobradiças, pois serão possíveis pontos de quebra para analisarmos grelhas simples
- Quebrar essas rótulas e dobradiças e substituir por apoios fictícios
- Analisar se as treliças formadas são simples e isostáticas
- Definir o melhor apoio para estrutura (alguns professores deixam um apoio faltando e pedem para o aluno dizer qual seria o melhor apoio para aquela estrutura)
- Pegar todas as reações de apoios fictícios e transferir para as barras em que eles se apoiam
- Definir uma ordem de solução
- Calcular as reações de apoio
- Calcular os diagramas
Dito isso tudo, vamos aplicar nosso passo a passo na grelha do nosso problema.
Passo 2
Como vimos primeiro devemos achar as possíveis rótulas a serem rompidas, e no nosso exemplo só temos uma possível chance de rompimento, na rótula, que marcamos aqui em baixo.
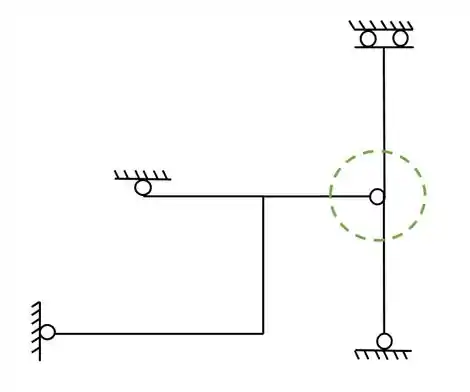
se lembrarmos o que vimos na aula teórica, lembraremos que o rompimento de rótulas gera apoios do primeiro gênero, e o rompimento de dobradiças, geram também, dobradiças.
Porém, vamos ao próximo passo então.
Passo 3
O segundo passo consiste em olharmos a nossa estrutura separada e com o apoio fictício
- Rompendo a Rótula teremos que
Perceba que ao romper a rótula teremos a seguinte estrutura
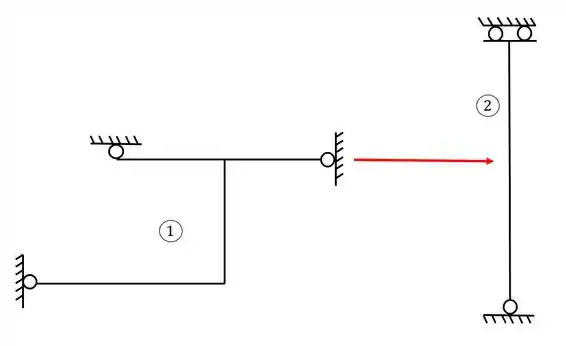
Fazendo o balanceamento de equações e incógnitas da primeira estrutura (mais a esquerda) veremos que ela possui 3 apoios do primeiro gênero, logo, possui 3 incógnitas, já que cada apoio gera uma incógnita. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.
Já a segunda estrutura (mais a direita) nós vemos que possui 1 apoio do primeiro gênero que nos dá 1 incógnita e um apoio do segundo gênero que nos dá 2 incógnitas. Dessa forma temos ao todo 3 equações, e 3 incógnitas, ou seja, de fato as nossas duas estruturas mais simples estão devidamente divididas.
Passo 4
Antes de resolver precisamos fazer a ordem de solução. Já sabemos que a primeira estrutura a ser resolvida é aquela que se apoia, e em seguida resolvemos as estruturas que servem de apoio, dessa forma nossa ordem de solução será.
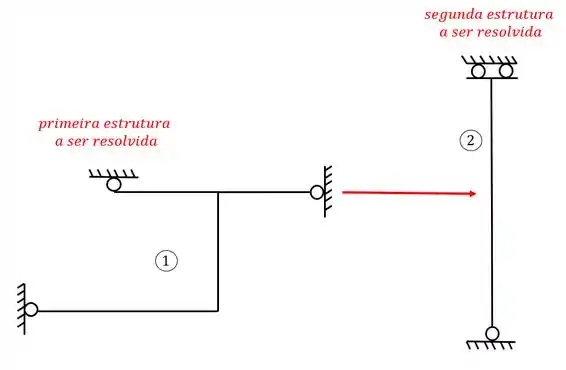
Passo 5
Definido tudo isso vamos resolver o nosso problema, calculando as reações de apoio necessária, começando primeiro pela estrutura mais a esquerda, para isso faremos o seguinte.
Como já vimos as nossas estruturas estão devidamente balanceadas, então devemos trocar os nossos apoios por reações nos sentidos e direções corretas, dessa forma a nossa estrutura ficará da seguinte maneira
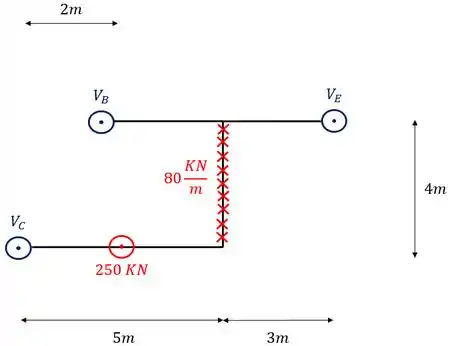
Sabemos que na sequência de passos, devemos trocar todas as cargas distribuídas por cargas concentradas, dessa forma, teremos que
- BARRA COM CARGA DISTRIBUÍDA
- Apoio A
- Apoio B
Para isso apenas precisamos fazer o seguinte cálculo
Dessa forma a nossa barra ficará da seguinte maneira
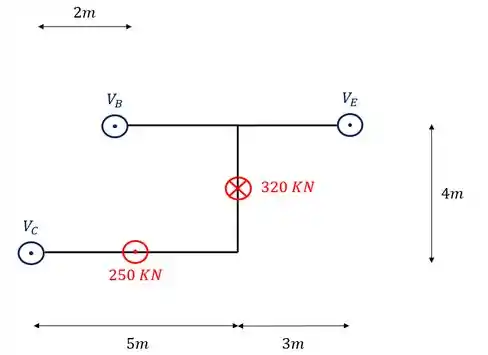
Passo 6
Sabemos que o cálculo das reações de apoio usará as formulas de equilíbrio que destacamos lá em cima, mas temos que tomar muito cuidado com os braços de alavanca, por isso vamos tomar bastante cuidado, vamos fazer cada fórmula de cada vez
Sabemos que para termos equilíbrio devemos saber que o somatório de momentos em qualquer ponto da nossa barra deve ser zero, com isso, o ponto que iremos escolher é o ponto C. Dessa forma teremos
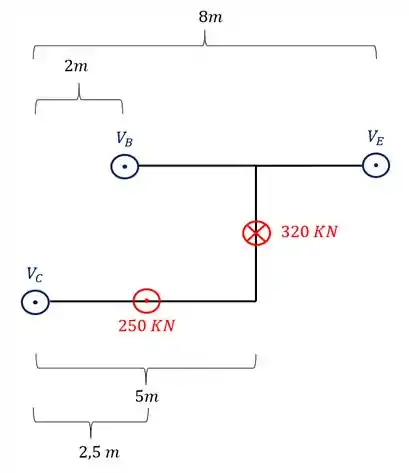
Perceba que nesse caso, todos os braços de alavancas de momento fletor, são perpendiculares ao apoio, todas as forças devem multiplicar o braço de alavanca correspondente. Com relação aos sinais eu arbitro positivo pra cima e negativo pra baixo, mas você tem liberdade da escolha dos sinais. Sabendo de tudo isso, o nosso equilíbrio de momentos fletores será
Mudando o sinal e simplificando teremos que
Vamos a próxima equação de equilíbrio.
Usando agora o equilíbrio de momentos torsores em C teremos que
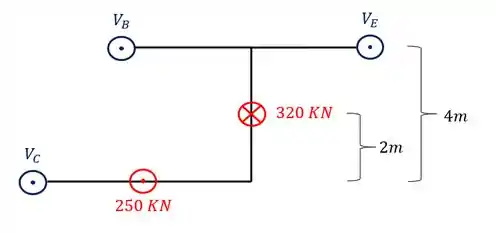
Com relações aos sinais eu considero positivo todos os torques que estiverem pra direita e negativo todos que estiverem para esquerda. Assim sendo teremos que
Substituindo no primeiro sistema teremos que
Nesse caso não precisamos de braços de alavancas, só somar e subtrair as forças, considerando sair do papel positivo e entrar no papel negativo, teremos que
Como deu negativo, basta invertermos o vetor para usarmos o valor positivo. Como já temos todas as reações teremos que
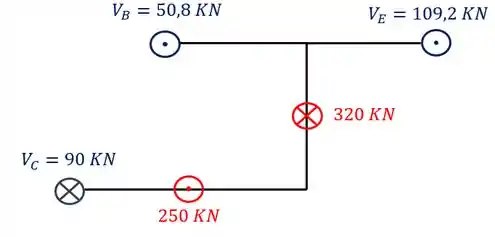
Passo 7
Agora temos que transferir a carga do apoio fictício para a segunda estrutura, lembrando sempre de inverter o sentido do vetor, dessa forma teremos que
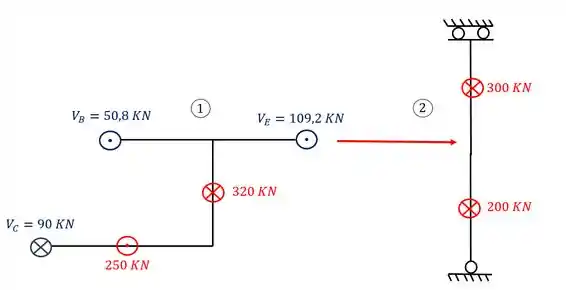
Agora que transferimos, basta descartamos a primeira parte e resolver apenas a segunda, dessa forma resolveremos totalmente o nosso exercício.
Passo 8
Como vimos, na sequência de passos, devemos trocar o nosso apoio por reações nos sentidos e direções corretas, dessa forma a nossa estrutura ficará da seguinte maneira
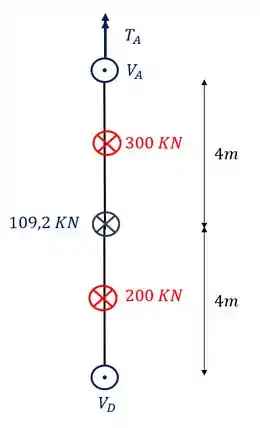
Passo 10
O próximo passo da nossa sequência é exatamente o cálculo das reações de apoio. Sabemos que o cálculo das reações de apoio usará as formulas de equilíbrio que destacamos lá em cima, mas temos que tomar muito cuidado com os braços de alavanca, por isso vamos tomar bastante cuidado, vamos fazer cada fórmula de cada vez
Sabemos que para termos equilíbrio devemos saber que o somatório de momentos em qualquer ponto da nossa barra deve ser zero, com isso, o ponto que iremos escolher é o ponto A que representa o nosso apoio. Dessa forma teremos
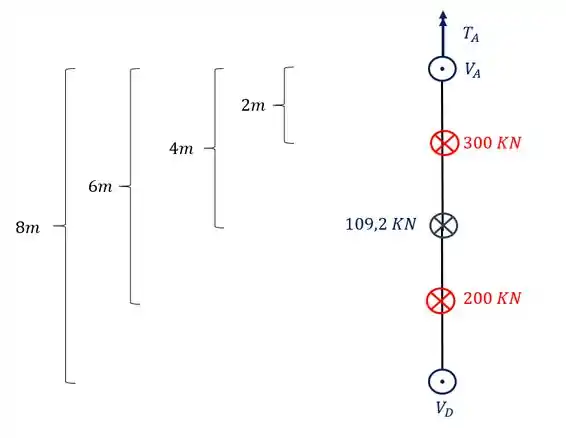
Perceba que nesse caso, todos os braços de alavancas de momento fletor, são perpendiculares ao apoio, todas as forças devem multiplicar o braço de alavanca correspondente. Com relação aos sinais eu arbitro positivo pra direita e negativo pra esquerda, mas você tem liberdade da escolha dos sinais. Sabendo de tudo isso, o nosso equilíbrio de momentos fletores será
Nesse caso não precisamos de braços de alavancas, só somar e subtrair as forças, considerando sair do papel positivo e entrar no papel negativo, teremos que
E o somatório dos torques podemos ver que é zero, logo
Assim temos todas as reações de apoios, que são dadas por
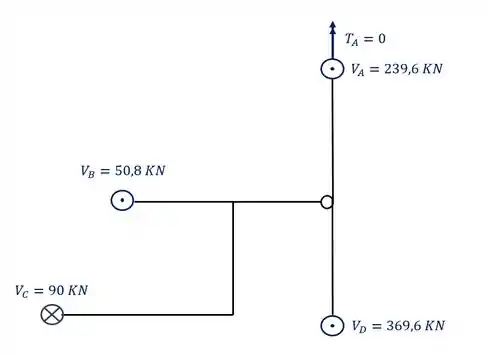
Resposta
Reações de apoio
Resposta
Ei, a resposta está no passo a passo :)