Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Ciclo Diesel

Ver Todos os Exercícios

Teoria

Fala aí! Bora aprender um pouquinho mais sobre o Ciclo Diesel? Este ciclo é a base de funcionamento dos motores presentes na grande maioria dos veículos para carga pesada e apresenta algumas vantagens em relação ao Ciclo Otto.

⭐Não deixe de conferir também⭐

Como funciona o Ciclo Diesel?

Quando estudamos o Ciclo Otto, aquele do motor dos carros movidos a gasolina ou álcool, vemos que cada pistão possui uma vela de ignição responsável por gerar uma centelha que causa a ignição do combustível. Aqui no Ciclo Diesel não precisa disso! A pressão extremamente alta dentro do cilindro provoca a autocombustão do combustível.

Bora ver isso aí com um pouquinho mais de detalhes. Vamos dividir o funcionamento de um motor a diesel em 4 etapas:

  1. Admissão 👉 Nesta etapa ocorre a admissão de ar no cilindro. O pistão se desloca do PMS (Ponto Morto Superior, é o ponto mais alto que o pistão pode alcançar) para o PMI (Ponto Morto Inferior, o ponto mais baixo).
  2. Compressão 👉 Nesta etapa ocorre a compressão do ar dentro do cilindro. O pistão se desloca do PMI para o PMS. Essa compressão produz uma elevação da temperatura na câmara de combustão, que pode chegar a até 800 ºC 🔥. No fim desta etapa, ocorre a injeção de combustível na câmara, e o combustível entra em combustão imediatamente devido ao contato com o ar aquecido.
  3. Expansão 👉 Aqui ocorre a combustão da mistura de ar e combustível. A expansão dos gases devido à combustão força o pistão do PMS para o PMI. Isso provoca uma transformação de energia térmica para mecânica, que é o que irá promover o movimento do veículo. Esta etapa é a única em que ocorre transformação de energia.
  4. Descarga 👉 Nesta etapa o pistão se desloca do PMI para o PMS, empurrando os resíduos da combustão 💨 para fora do cilindro por meio da válvula de descarga.

Etapas do Ciclo Diesel

Agora vamos olhar para essas etapas de um ponto de vista mais termodinâmico, que é o que mais importa mesmo.

Para isso, vamos olhar pra esse gráfico aqui e analisar cada uma das etapas:

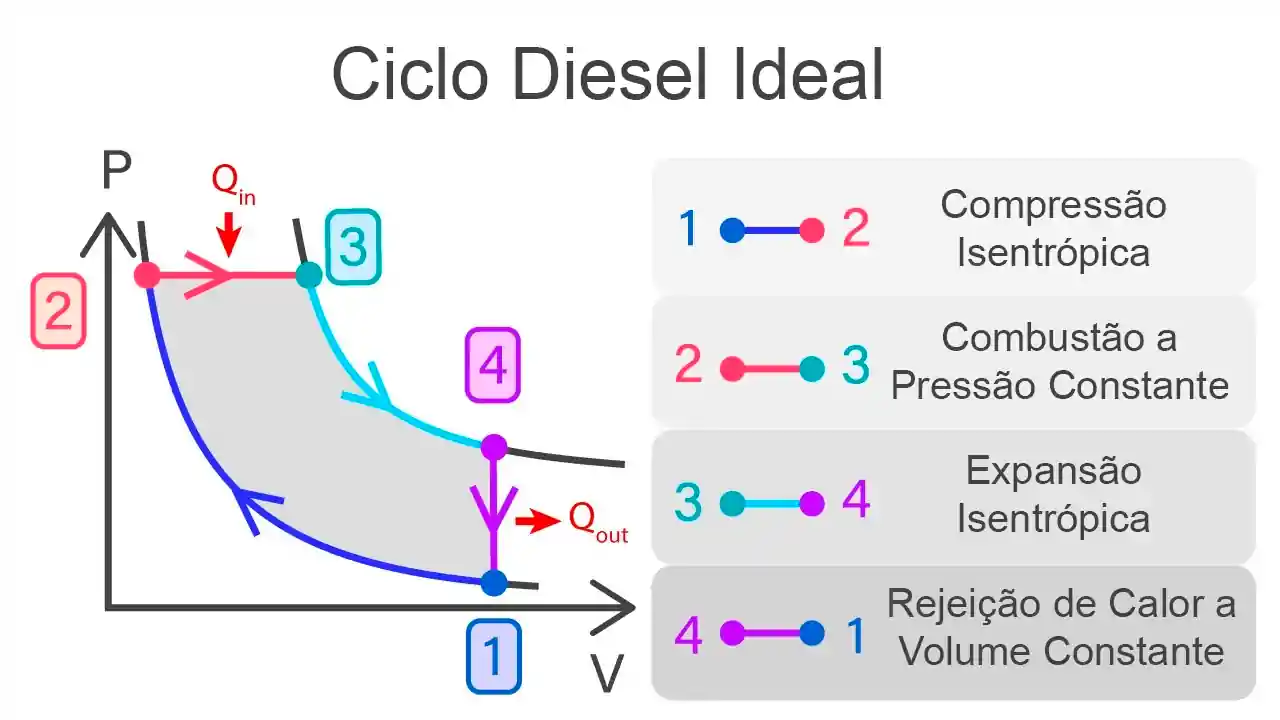
Gráfico Pressão X Volume para o Ciclo Diesel.
Gráfico Pressão X Volume para o Ciclo Diesel.

1 - 2: Compressão Isentrópica

Ali em é onde ocorre a admissão. Do ponto para o , o pistão sobe e comprime o ar dentro do cilindro em uma compressão isentrópica (lembrando que um processo isentrópico é um processo adiabático reversível, em que não há troca de calor.

2 - 3: Combustão a Pressão Constante

Aquela setinha com um ali em cima indica que houve a adição de calor no sistema. Esse calor vem por meio da combustão em um processo isobárico.

3 - 4: Expansão Isentrópica

O pistão desce e provoca a expansão do ar em um processo isentrópico.

4 - 1: Rejeição de Calor a Volume Constante

Neste processo ocorre a exaustão de calor, , por meio de um processo isovolumétrico.

Em um resuminho bem básico, temos duas isentrópicas, uma isobárica e uma isovolumétrica!

Diferenças entre o Ciclo Diesel e o Ciclo Otto

A diferença mais clássica entre os motores a diesel e os a gasolina é o modo como ocorre a combustão. Enquanto o motor a gasolina requer o acionamento de uma vela de ignição, o motor a diesel faz isso só por meio da compressão do combustível.

Mas existem outras diferenças também! Durante a etapa de admissão do Ciclo Otto, ocorre a entrada de uma mistura de ar e combustível na câmara de combustão, isso provoca perdas na taxa de compressão do motor. O Ciclo Diesel evita isso ao admitir somente ar durante sua primeira etapa e injetar o combustível somente quando o sistema estiver sob máxima compressão.

Do ponto de vista termodinâmico, podemos olhar para os gráficos dos dois ciclos lado a lado para perceber a principal diferença logo de cara:

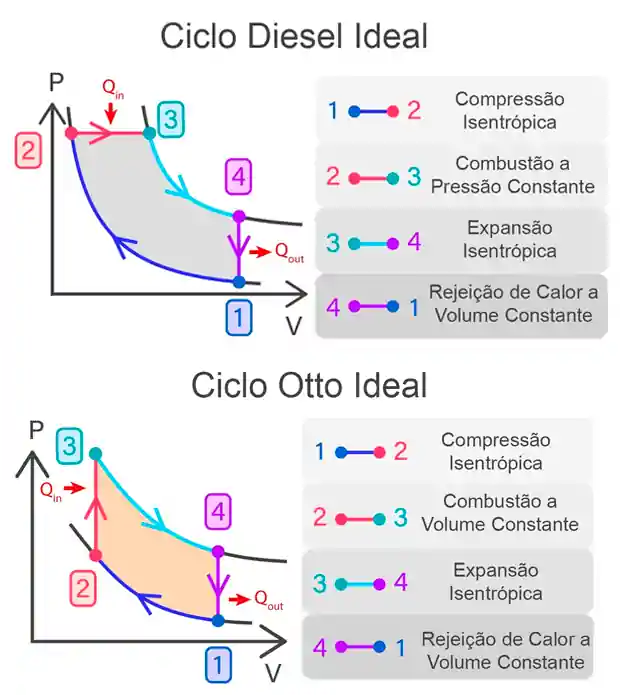
Comparação entre Ciclo Diesel e Ciclo Otto.
Comparação entre Ciclo Diesel e Ciclo Otto.

Repare que a grande diferença ocorre ali na etapa em que há a adição de calor. A entrada de calor no Ciclo Diesel ocorre a pressão constante, já no Ciclo Otto ela ocorre a volume constante.

O primeiro ciclo é composto por duas isentrópicas, uma isobárica e uma isovolumétrica. O segundo possui duas isovolumétricas e duas isentrópicas.

A velocidade de queima do combustível no Ciclo Diesel é mais lenta que a do Ciclo Otto, isso permite que o trabalho e o torque gerado pelos motores a diesel sejam maiores.

Bora ver como se calcula a eficiência do Ciclo Diesel e como ela se compara ao Otto?

Eficiência do Ciclo Diesel

Pra calcular a eficiência do Ciclo Diesel não tem muito segredo não. Vamos usar aquela definição de que eficiência é a relação entre a energia fornecida a um sistema e a energia produzida pelo sistema .

Aplicando a primeira lei da termodinâmica, chegamos em:

Essa expressão é até bonitinha, mas ela sozinha não vai resolver todos os nossos problemas. Por isso, podemos fazer algumas manipulações e chegar na seguinte expressão:

Calma, não se assusta! Apesar dessa expressão ser bem mais feia, ela é um tanto quanto útil!

Olha só, é a razão de compressão, e é definida como o volume do ponto lá no gráfico do ciclo dividido pelo volume do ponto . Chamamos de razão de corte aquele , e ele equivale à razão entre o volume do ponto e o do ponto . E aquele meio engraçado ali é a letra grega gamma , que representa a razão entre os calores específicos.

Agora olha que interessante, quando comparamos essa expressão da eficiência do Ciclo Diesel com aquela da eficiência do Ciclo Otto:

Percebemos que a eficiência teórica do Ciclo Otto vai ser sempre maior que a do Diesel para uma determinada taxa de compressão . Maaaas isso não se mantém verdade para o mundo real, já que o os motores a diesel são capazes de operar com taxas de compressão muito mais altas.

Etapas do Ciclo Diesel

Diferenças entre o Ciclo Diesel e o Ciclo Otto

Eficiência do Ciclo Diesel

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Abaixo estão representadas as fórmulas para cálculo das eficiências de um ciclo Otto e um ciclo Diesel. Observando as duas equações pode-se perceber que a eficiência de um ciclo Diesel é sempre menor do que a do Otto para uma mesma razão de compressão r . Explique, então, porque o ciclo Diesel é considerado mais eficiente do que o ciclo Otto e porque é mais utilizado em veículos de grande porte.

η O t t o = 1 - 1 r γ - 1  

η D i e s e l = 1 - 1 γ ⋅ ( r c γ - 1 ) r γ - 1 ⋅ ( r c - 1 )

Passo 1

Como r c (razão de corte) é igual a razão entre os pontos 3 e 2 (depois e antes do combustível ser injetado) então r c > 1 com isso a eficiência do ciclo Diesel realmente é menor do que a do ciclo Otto.

Porém, é crucial notar que isso é válido apenas para o caso de uma mesma razão de compressão r . Como a razão de compressão do ciclo Diesel (15 até 25) é bem maior do que a do ciclo Otto (8 até 12) então no final das contas o ciclo Diesel é mais eficiente.

Passo 2

Pelo fato do ciclo Diesel ter uma combustão mais lenta do que o ciclo Otto, o ciclo Diesel terá um torque maior, fundamental para veículos de grande porte, enquanto o ciclo Otto terá uma potência maior, ideal para carros de corrida por exemplo.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

Elaboração própria

O cálculo da eficiência de um ciclo Diesel pode ser calculado conforme a equação abaixo:

η = 1 - 1 γ ⋅ ( r c γ - 1 ) r γ - 1   ( r c - 1 )

Porém além disso, pode ser calculado como qualquer motor termodinâmico, ou seja, da forma:

η = w q h = 1 - q L q H

Se fosse viável saber a temperatura de cada ponto desse ciclo descreva como ficaria essa relação em função das temperaturas.

Passo 1

Aqui o mais importante é lembrar que o ciclo Diesel recebe calor a pressão constante e perde calor a volume constante. Isso é importante porque o calor trocado a pressão constante é dado por:

q = c p Δ T

E a volume constante é igual a

q = c v Δ T

Ou seja,

q H = c p Δ T 3 - 2

q L = c v Δ T 4 - 1

Assim,

η = 1 - c v ( T 4 - T 1 ) c p ( T 3 - T 2 )

É claro que é muito difícil obter todas essas temperaturas, por isso é muito mais conveniente utilizar a relação de volumes.

Resposta

η = 1 - c v ( T 4 - T 1 ) c p ( T 3 - T 2 )

Exercício Resolvido #3

Elaboração própria

Um motor funciona segundo o ciclo Diesel e possui razão de compressão igual a 20, razão de corte igual a 3 e na primeira etapa de seu ciclo (compressão) a pressão é igual a 100 kPa e temperatura de 20°C. Calcule a temperatura ao final da compressão, a eficiência desse ciclo e a pressão efetiva média, sabendo que esse ciclo absorve um q h = 1500 k J k g . Dado: R a r = 0,287 k J k g   K

Passo 1

A temperatura ao final da compressão pode ser calculada pela relação isentrópica:

T 2 T 1 = v 1 v 2 γ - 1

T 2 20 + 273 = 20 1,4 - 1

T 2 = 293 ⋅ 3,314 = 971 K

Passo 2

A eficiência do ciclo Diesel é definida como:

η = 1 - 1 γ ⋅ ( r c γ - 1 ) r γ - 1   ( r c - 1 )

Portanto, a eficiência será igual a

η = 1 - 1 1,4 ⋅ 3 1,4 - 1 20 1,4 - 1 ⋅ 2 = 1 - 0,714 ⋅ 3 , 655 6,623 = 60,6 %

Passo 3

A pressão efetiva média é dada por

p m e = w l i q ( v 1 - v 2 )

Portanto, vamos precisar achar w l i q , v 1 e v 2

Vamos achar primeiro o trabalho líquido que é dado por

η = w l i q q h

w l i q = η ⋅ q h = 0,606 ⋅ 1500 = 909 k J k g

Agora achamos os volumes por meio da equação de Clapeyron

P v = R T

v 1 = R T 1 p 1 = 0,287 ⋅ 293 100 = 0,841 m 3 k g

v 2 = v 1 20 = 0,841 20 = 0,042 m 3 k g

Agora é só substituir

p m e = w l i q ( v 1 - v 2 )

p m e = 909 ( 0,841 - 0,042 ) = 1137,67   k P a

Resposta

T 2 = 971 K

η = 60,6 %

p m e = 1137,67     k P a

Exercício Resolvido #4

UNICAMP, Termodinâmica, Prof. Dr. Ricardo A. Mazza, p. 1 (Adaptada)

Um motor ciclo Diesel ideal opera com uma razão de compressão de 20 usa ar como fluido de trabalho. O estado do ar no começo da compressão é de 95kPa e 20°C. Se a máxima temperatura do ciclo não deve exceder 2200K, determine a eficiência térmica

Considere que as propriedades são constantes à temperatura ambiente.

Dados: c v = 0,718 k J k g   K ; γ = 1,4 ; R a r = 287 J k g   K ; c p = 1,0035 k J k g   K

Passo 1

Se a temperatura não deve exceder 2200K isso significa que T 3 = 2200 K então projetaremos o motor para tal. Se conseguirmos achar a razão de corte então nossa vida irá simplificar muito.

Primeiro vamos achar T 2

T 2 T 1 = V 1 V 2 γ - 1

T 2 20 + 273 = 20 1,4 - 1

T 2 = 293 ⋅ 20 0,4 = 971 K

Para achar T 4 temos de saber primeiro o volume V 3 que é dado pela relação dos gases perfeitos a pressão constante

V 3 T 3 = V 2 T 2

V 3 V 2 = T 3 T 2 = 2200 971 = 2,265

Passo 2

Observe que essa relação é exatamente a razão de corte r c do motor. Então podemos substituir direto na equação da eficiência

η = 1 - 1 γ ⋅ ( r c γ - 1 ) r γ - 1 ( r c - 1 )

η = 1 - 1 1,4 ⋅ ( 2,265 1,4 - 1 ) 20 0 , 4 ( 2,265 - 1 )

η = 1 - 0,714 ⋅ 2,14 3,314 ⋅ 1,265 = 1 - 0,364 = 63,5 %

Resposta

η = 63,5 %

Exercício Resolvido #5

Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.298 – Exercício 9.62 (adaptada).

Considere um ciclo padrão a ar Diesel ideal, no qual o estado do ar, antes do processo de compressão, é 90 kPa e 290K e a relação de compressão é 20. Qual deve ser a máxima temperatura do ciclo para que o rendimento térmico seja igual a 60,6%? Dados: γ a r = 1,4

Passo 1

Vamos olhar a equação da eficiência antes de começar a resolver o problema

η = 1 - 1 γ ⋅ ( r c γ - 1 ) r γ - 1 ⋅ ( r c - 1 )

Como já temos o fator de compressão r basta e sabemos também que r c = V 3 V 2 . Aí a gente lembra que a operação 2 – 3 é uma isobárica e, portanto, a relação

V 3 V 2 = T 3 T 2

É válida

Passo 2

Então o que vamos fazer aqui é calcular o r c

60,6 % = 1 - 1 1,4 ⋅ ( r c 1,4 - 1 ) 20 1,4 - 1 ⋅ ( r c - 1 )

1 1,4 ⋅ r c 1,4 - 1 20 1,4 - 1 ⋅ r c - 1 = 0,394

r c 1,4 - 1 r c - 1 = 0,394 ⋅ 1,4 ⋅ 20 0,4

r c 1,4 - 1 r c - 1 = 1,828

Aqui vamos ter que chutar alguns valores de r c , lembrando é claro que r c não pode ser igual a 1. Portanto, se colocarmos r c = 2 temos:

2 1,4 - 1 2 - 1 = 1,639

r c = 3

3 1,4 - 1 3 - 1 = 1,827

A aproximação r c = 3 está bem próxima, portanto, vamos utiliza-la.

Passo 3

Agora vamos achar a temperatura T 2 por meio da relação das isentrópicas

T 2 T 1 = V 1 V 2 γ - 1

T 2 = 290 ⋅ 20 0 , 4 = 961 K

Passo 4

Vamos achar T 3 pela relação da isobárica (proveniente da equação de Clapeyron)

V 3 V 2 = r c = T 3 T 2

3 = T 3 961

T 3 = 961 ⋅ 3 = 2883 K

Resposta

T 3 = 2883 K

Exercício Resolvido #6

Elaboração própria

Um ciclo padrão a ar Diesel ideal, no qual o estado do ar, antes do processo de compressão, é 90 kPa e 290K e a relação de compressão é 20 e o fator de corte igual a 2,5. Calcule o calor frio trocado, o calor quente recebido, o trabalho líquido e a eficiência deste ciclo. Dados: γ a r = 1,4 . c p = 1,0035 k J k g   K ; c v = 0,7165 k J k g   K

Passo 1

Se acharmos a temperatura em cada um dos estados então será fácil achar os calores e trabalho porque os calores dependem da variação da temperatura e do fluido, no caso o ar. Então vamos achar a temperatura T 2 por meio da relação das isentrópicas

T 2 T 1 = V 1 V 2 γ - 1

T 2 = 290 ⋅ 20 0 , 4 = 961 K

Passo 2

A temperatura T 3 nós vamos achar pela relação da isobárica, lembrando que V 3 V 2 = r c

V 3 V 2 = T 3 T 2

r c = T 3 T 2

2,5 = T 3 961

T 3 = 961 ⋅ 2,5 = 2402,5 K

Passo 3

Agora vamos achar a temperatura T 4 novamente por meio da relação das isentrópicas

T 4 T 3 = V 3 V 4 γ - 1

O probleminha aqui é a relação V 3 / V 4 mas a gente sabe que V 4 = V 1 e sabemos também que

V 1 V 2 = r

V 3 V 2 = r c

Então

V 4 V 3 = V 1 V 3 = r r c

Assim,

T 4 T 3 = r c r γ - 1

T 4 = 2402,5 ⋅ 2,5 20 0,4 = 1045,7 K

Passo 4

Agora basta achar q H e q L .

q H = c p Δ T 3 - 2

q H = 1,0035 ⋅ 2402,5 - 961 = 1446,54 k J k g

q L = c v Δ T 4 - 1

q L = 0,7165 ⋅ 1045,7 - 290 = 541,46 k J k g

Passo 5

Então w l i q é igual a

w l i q = 1446,54 - 541,46 = 905,08 k J k g

E a eficiência

η = w l i q q H = 905,08 1446,54 = 62,6 %

Resposta

q H = 1446,54 k J k g

q L = 541,46 k J k g

w l i q = 905,08 k J k g

η = 62,6 %

Exercício Resolvido #7

Michael J. Moran, Howard N. Shapiro, Daisied Boettner e Margaret B. Bailey, Princípios de termodinâmica para engenhanaria, Tradução da 7ª ed. americana. Rio de Janeiro: LTC, 2013, pp.454 – Exercício 9.31.

No início da compressão de um ciclo de ar-padrão Diesel, p 1 = 170   k P a , V 1 = 0,016   m ³ e T 1 = 315   K . A taxa de compressão é 15 e a temperatura máxima do ciclo é de 1400K. Determine. Dado: c v a r = 0,7 2 k J k g   K ; c p = 1,0048 k J k g   K γ a r = 1,4 , R a r = 0,287 k J k g   K .

a) A massa de ar, em kg.

b) A adição e a rejeição de calor por ciclo.

c) O trabalho líquido e a eficiência térmica.

Passo 1

Vamos calcular a massa de ar pela equação dos gases perfeitos na forma:

P V = m R T

A massa aparece aqui porque estamos utilizando o volume absoluto (em m³) ao invés do volume específico (em m³/kg) e também por estarmos utilizando a constante R relativa ao ar, que já considera a massa molecular desta susbtância. Portanto, a massa pode ser calculada como:

m = P V R T = 170 ⋅ 0,016 0,287 ⋅ 315 = 0,03   k g

Passo 2

Para achar o calor quente (adição de calor) e o calor frio (rejeição) vamos utiliazar as equações para troca de calor em isobáricas (adição) e isovolumétricas (rejeição), isso para o caso do Diesel.

Q H = m c p Δ T 2 - 3

Repare que utilizamos Q maiúsculo quando a massa entra na equação, pois resultará na quantidade de calor de fato (ao invés da quantidade de calor pela massa).

Então vamos calcular as temperaturas em 2 e em 3 para substituir na fórmula. Como o processo 1 – 2 é uma isentrópica então

T 2 T 1 = v 1 v 2 γ - 1

T 2 315 = 15 1,4 - 1

T 2 = 315 ⋅ 15 0,4 = 930 K

Da mesma forma para o processo 3 – 4

T 4 T 3 = V 3 V 4 γ - 1

A relação V 3 V 4 pode ser obtida a partir do processo 3 – 2 (isobárica) e vamos ter:

V 3 T 3 = V 2 T 2

V 3 V 2 = T 3 T 2

Repara que essa relação dos volumes é igual à razão de corte

r c = V 3 V 2 = T 3 T 2 = 1400 930 = 1,5

E lembrando que o fator de compressão é dado por

r = V 1 V 2

E que V 1 = V 4 , vamos ter

r = V 4 V 2

Então a relação entre V 3 e V 4 fica da forma

V 3 V 4 = r c r

Voltando na fórmula

T 4 T 3 = r c r γ - 1

T 4 = 1400 ⋅ 1,5 10 1,4 - 1 = 557 K

Passo 3

Agora que temos as temperaturas fica facinho facinho achar os calores:

Q H = m c p Δ T 2 - 3

Q H = 0,03 ⋅ 1,0048 ⋅ 1400 - 930 = 14,14   k J

Q L = m c v Δ T 4 - 1

Q L = 0,03 ⋅ 0,72 ⋅ 557 - 315 = 5,23 k J

Passo 4

E o trabalho líquido será dado por

W l i q = Q H - Q L

W l i q = 14,14 - 5,23 = 8,91   k J

E a eficiência

η = W l i q Q H

η = 8,91 14,14 = 63 %

Resposta

m = 0,03   k g

Q H = 0,03 ⋅ 1,0048 ⋅ 1400 - 930 = 14,14   k J

Q L = 0,03 ⋅ 0,72 ⋅ 557 - 315 = 5,23 k J

W l i q = 8,91   k J

η = 63 %

Exercício Resolvido #8

Michael J. Moran, Howard N. Shapiro, Daisied Boettner e Margaret B. Bailey, Princípios de termodinâmica para engenhanaria, Tradução da 7ª ed. americana. Rio de Janeiro: LTC, 2013, pp.454 – Exercício 9.24.

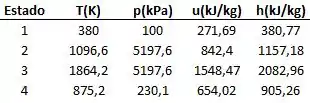
Considere um ciclo de ar-padrão Diesel. Os dados operacionais são fornecidos em seus estados principais no ciclo na tabela a seguir. Determine

a) A razão de corte.

b) O calor adicionado por unidade de massa.

c) O calor rejeitado por unidade de massa.

d) O trabalho líquido.

e) A eficiência térmica.

Passo 1

Vamos calcular a massa de ar pela equação dos gases perfeitos na forma:

P V = m R T

A massa aparece aqui porque estamos utilizando o volume absoluto (em m³) ao invés do volume específico (em m³/kg) e também por estarmos utilizando a constante R relativa ao ar, que já considera a massa molecular desta susbtância. Portanto, a massa pode ser calculada como:

m = P V R T = 170 ⋅ 0,016 0,287 ⋅ 315 = 0,03   k g

Passo 2

Para achar o calor quente (adição de calor) e o calor frio (rejeição) vamos utiliazar as equações para troca de calor em isobáricas (adição) e isovolumétricas (rejeição), isso para o caso do Diesel.

Q H = m c p Δ T 2 - 3

Repare que utilizamos Q maiúsculo quando a massa entra na equação, pois resultará na quantidade de calor de fato (ao invés da quantidade de calor pela massa).

Então vamos calcular as temperaturas em 2 e em 3 para substituir na fórmula. Como o processo 1 – 2 é uma isentrópica então

T 2 T 1 = v 1 v 2 γ - 1

T 2 315 = 15 1,4 - 1

T 2 = 315 ⋅ 15 0,4 = 930 K

Da mesma forma para o processo 3 – 4

T 4 T 3 = V 3 V 4 γ - 1

A relação V 3 V 4 pode ser obtida a partir do processo 3 – 2 (isobárica) e vamos ter:

V 3 T 3 = V 2 T 2

V 3 V 2 = T 3 T 2

Repara que essa relação dos volumes é igual à razão de corte

r c = V 3 V 2 = T 3 T 2 = 1400 930 = 1,5

E lembrando que o fator de compressão é dado por

r = V 1 V 2

E que V 1 = V 4 , vamos ter

r = V 4 V 2

Então a relação entre V 3 e V 4 fica da forma

V 3 V 4 = r c r

Voltando na fórmula

T 4 T 3 = r c r γ - 1

T 4 = 1400 ⋅ 1,5 10 1,4 - 1 = 557 K

Passo 3

Agora que temos as temperaturas fica facinho facinho achar os calores:

Q H = m c p Δ T 2 - 3

Q H = 0,03 ⋅ 1,0048 ⋅ 1400 - 930 = 14,14   k J

Q L = m c v Δ T 4 - 1

Q L = 0,03 ⋅ 0,72 ⋅ 557 - 315 = 5,23 k J

Passo 4

E o trabalho líquido será dado por

W l i q = Q H - Q L

W l i q = 14,14 - 5,23 = 8,91   k J

E a eficiência

η = W l i q Q H

η = 8,91 14,14 = 63 %

Resposta

m = 0,03   k g

Q H = 0,03 ⋅ 1,0048 ⋅ 1400 - 930 = 14,14   k J

Q L = 0,03 ⋅ 0,72 ⋅ 557 - 315 = 5,23 k J

W l i q = 8,91   k J

η = 63 %

Exercícios de Livros Relacionados

Refaça o Prob. 11.106 utilizando as propriedades do ar indicadas na Tab. A.7.
Um motor Diesel, com seis cilindros, utiliza pistões com diâmetros iguais a 100m m . O curso dos pistões é 110m m e a relação de compressão deste motor é 19 : 1 . Normalmente, o motor opera a 2000r p
A temperatura e a pressão do ar antes do processo de compressão num motor diesel são iguais a 290K e 95k P a . Sabendo que a pressão e a temperatura máximas no ciclo são iguais a 6M P a e 2400K , dete
O ciclo ideal a ar de Carnot não foi mostrado neste texto. Construa um diagrama T - s para este ciclo. Admitindo que a temperatura mínima neste ciclo seja 280K , que a eficiência térmica seja 60 % e q
Considere um motor Stirling ideal no qual a pressão e a temperatura no início do processo de compressão isotérmica são iguais a 100k P a e 25 ° C . Sabendo que a relação de compressão é 6 e que a temp