Teoria
O ciclo Otto
Agora vamos ver um ciclo muito importante no estudo da termodinâmica, o ciclo Otto, que é o ciclo utilizado nos motores de combustão interna de ignição por centelha, aquele utilizado nos carros movidos a gasolina ou álcool. Nesse ciclo, embora exista uma mistura de ar com a gasolina e os produtos da combustão, dizemos que o fluido de trabalho é o ar e funciona basicamente assim:
- 1 – 2: O pistão sobe comprimindo o ar existente no cilindro numa compressão isentrópica.
- 2 – 3: A centelha é acionada e a mistura de ar e combustível entre em combustão fornecendo calor para o ar num processo isovolumétrico.
- 3 – 4: O pistão desce fazendo com que o ar se expanda num processo de expansão isentrópica.
- 4 – 1: Rejeição de calor a volume constante, ou seja, um processo isovolumétrico.
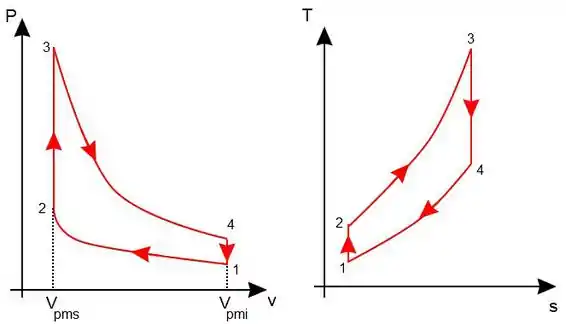
Obs: Os pontos Vpms e Vpmi representam o volume do ponto morto superior, quando o pistão se encontra no ponto mais alto, e o volume do ponto morto inferior, quando o pistão se encontra no ponto mais baixo, respectivamente.
Então é legal lembrar que esse ciclo é composto por duas isovolumétricas e duas isentrópicas.
Eficiência
A eficiência do ciclo Otto é calculada como qualquer outra eficiência de uma máquina térmica.
Como, pela primeira lei:
Vamos ter que a eficiência pode ser escrita da forma:
Aí é legal ver que o ciclo recebe calor (processo 2 – 3) e rejeita calor (processo 4 – 1) numa isovolumétrica. Como o calor trocado durante uma isovolumétrica é calculado da forma , então podemos escrever a eficiência assim:
Isso aí de cima é igual a
Onde é a chamada razão de compressão e é definida como , que também é igual a . É legal ver que eficiência do ciclo de Otto depende apenas da razão de compressão!
Okay, você não faz ideia de onde isso surgiu né? Calma, eu vou explicar mais abaixo mas envolve algumas continhas chatas, por isso dei logo o resultado que queremos.
Relações de temperatura e volume
Voltando aos cálculos vamos reorganizar isso:
colocando em evidência em cima e em evidência embaixo.
Aqui vamos ter que lembrar daquela relação para isentrópicas descrito no capítulo de ciclo de Brayton que diz:
A partir da equação de Clapeyron, na qual
Podemos escrever a pressão como
Assim
Como também é uma constante
Assim, se compararmos o ponto 1 com o ponto 2 temos:
Reorganizando e substituindo o volume específico pelo volume total .
Analogamente, para os pontos 3 e 4 temos que
Como a relação dos volumes entre os pontos 1 e 2 é a mesma que dos pontos 3 e 4.
Podemos escrever da forma
Logo achamos, também, uma relação entre temperaturas. Que pode ser escrita como
O que, finalmente, leva a uma simplificação da equação da eficiência.
Por fim, é mais prático colocar isso em função dos volumes já que são grandezas já especificadas no projeto do motor. Que leva a forma
Lembra que à razão dá-se o nome de razão de compressão, simbolizado pela letra . Vamos chegar na equação mostrada anteriormente
Relação de compressão e eficiência
Como visto anteriormente a eficiência aumenta quanto maior a relação de compressão. Isso pode ser visto no gráfico abaixo.
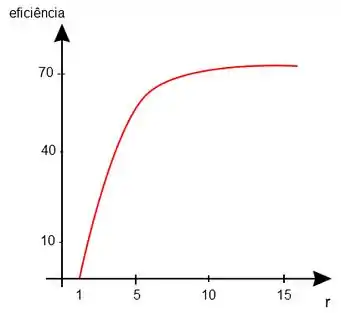
Porém existe um problema, na realidade no cilindro existe uma mistura de combustível e ar, e não somente ar como a teoria trabalha. Sendo assim, sob uma determinada pressão o combustível entra em combustão antes da hora certa (que seria a ignição por fagulha). Esse fenômeno é chamado de “Bater pino” e diminui a eficiência da máquina, além de causar outros problemas.
A relação de compressão do ciclo Otto gira varia de 8:1 até 12:1 mais ou menos, dependendo do combustível. Vale lembrar que o álcool admite compressões maiores do que a gasolina por exemplo.
Apesar disso o ciclo Otto consegue gerar grandes potências, ao contrário do ciclo Diesel, por exemplo, que vamos ver mais à frente, que gera grandes torques.
Pressão média efetiva
Às vezes podemos nos deparar com o termo pme, que é a pressão média efetiva. Não há nenhuma dificuldade nisso, basta lembrar que a pme é calculada como:
Uma forma de pensar sobre isso é fazendo a análise dimensional. Como tem unidade de pressão e estamos utilizando o trabalho líquido e a variação do volume, temos que uma pressão média.
Relações de temperatura e volume
Relação de compressão e eficiência
Pressão média efetiva
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um motor funciona segundo o ciclo Otto e possui razão de compressão igual a 10, sabendo que o ar possui qual a eficiência deste motor? É possível aumentar a eficiência apenas aumentando a razão de compressão? Se sim justifique porque o motor não pode trabalhar com razões de compressão muito elevadas.
Passo 1
Esse problema é bem direto e a eficiência do ciclo Otto depende exatamente da razão de compressão e é definida como:
Portanto, a eficiência será igual a
Passo 2
Sim, como dito no passo anterior a eficiência depende apenas da razão de compressão. Por isso aumentando essa razão a eficiência também aumenta.
Passo 3
Infelizmente não podemos aumentar a razão de compressão indefinidamente, porque ocorrerá o fenômeno da autocombustão onde o combustível entra em combustão devido à pressão elevada o que é conhecido também como “bater-pino” e é prejudicial ao motor.
Resposta
Exercício Resolvido #2
Elaboração própria
Um motor funciona segundo o ciclo Otto e possui razão de compressão igual a 8 e na primeira etapa de seu ciclo (compressão) a pressão é igual a 100 kPa e temperatura de 20°C. Calcule a temperatura ao final da compressão, a eficiência desse ciclo e a pressão efetiva média, sabendo que esse ciclo absorve um . Dado:
Passo 1
A temperatura ao final da compressão pode ser calculada pela relação isentrópica:
Passo 2
A eficiência do ciclo Otto depende exatamente da razão de compressão e é definida como:
Portanto, a eficiência será igual a
Passo 3
A pressão efetiva média é dada por
Portanto, vamos precisar achar , e
Vamos achar primeiro o trabalho líquido que é dado por
Agora achamos os volumes por meio da equação de Clapeyron
Agora é só substituir
Resposta
Exercício Resolvido #3
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.297 – Exercício 9.55.
Um motor a gasolina é alimentado com ar a 95 kPa e 300K. O ar então é comprimido num processo que apresenta relação de compressão volumétrica igual a 8 para 1. Sabendo que o combustível libera 1300 kJ/kg de energia térmica para o ar no processo de combustão, determine a temperatura e a pressão imediatamente após o processo de combustão. Dado:
Passo 1
Vamos anotar os dados da questão antes de começar a resolver:
Beleza, o que queremos então é a pressão e temperatura logo após a combustão, ou seja, o estado 3. Vamos lembrar que o processo 1 – 2 é isentrópico e 2 – 3 é isovolumétrico.
Passo 2
Como estamos falando de vários processos consecutivos é legal ir resolvendo o primeiro, depois o segundo, o terceiro e assim por diante. Desta forma vamos achando os dados de todos os estados. Então neste passo vamos achar a pressão e temperatura do estado 2, por meio daquelas relações isentrópicas:
Para a temperatura
Para a pressão
Passo 3
E agora, seguindo o caminho do ciclo vamos analisar o processo 2 – 3. Como este processo é um processo isovolumétrico, então a a transferência de calor é dada por:
Passo 4
Por último utilizaremos a relação de Clapeyron para achar a pressão no estado 3.
Resposta
Exercício Resolvido #4
Elaboração própria
Três motores de combustão interna operam segundo o ciclo Otto. Os motores são alimentados por gasolina, álcool e metanol, por este motivo as razões de compressão deles são distintas, de forma a se obter a maior eficiência possível. Sabendo que as razões de compressão para esses três motores são ; ; , compare a eficiência dos três motores.
Passo 1
Calcular a eficiência do ciclo por meio da equação
1 – Para a gasolina
Passo 2
Calcular a eficiência do ciclo por meio da equação
2 – Para o álcool
Passo 3
Calcular a eficiência do ciclo por meio da equação
3 – Para o metanol
Resposta
Logo, pode-se ver que quanto maior o fator de compressão do motor maior a eficiência. Um dos limitantes desta compressão é o tipo de combustível utilizado, já que alguns entram em autocombustão antes de outros.
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.297 – Exercício 9.56.
A relação de compressão de um motor a gasolina é de 9 para 1. O estado do ar antes da compressão é 290K e 90 kPa e a temperatura máxima do ciclo é de 1800K. Determine a pressão após a expansão, o trabalho líquido e a eficiência do ciclo. Dado: ;
Passo 1
Vamos anotar os dados da questão antes de começar a resolver:
O problema pede, a pressão após a expansão, o trabalho líquido e a eficiência do ciclo. Como a eficiência depende apenas da relação de compressão, esse vai ser nosso primeiro cálculo.
Passo 2
Calcular a eficiência do ciclo por meio da equação
Passo 3
Vamos achar a pressão e temperatura do estado 2, por meio daquelas relações isentrópicas:
Para a temperatura
Para a pressão
Passo 4
E agora, seguindo o caminho do ciclo vamos analisar o processo 2 – 3. Como este processo é um processo isovolumétrico, então a a transferência de calor é dada por:
Passo 5
Com a eficiência e o calor quente podemos achar o trabalho líquido
Passo 6
Utilizaremos a relação de Clapeyron para achar a pressão no estado 3.
Passo 7
Com a relação de pressão e volume para isentrópicas vamos achar a pressão após a expansão.
Resposta
Exercício Resolvido #6
UNICAMP, Termodinâmica, Prof. Dr. Ricardo A. Mazza, p. 2
A razão de compressão de motor ciclo Otto é de 9,5. O ar é admitido a 100kPa, 17°C e 600 cm3. A temperatura do processo no final da expansão isentrópica é de 800K. Utilizando os calores específicos a temperatura ambiente, determine:
a) a maior temperatura e pressão no ciclo
b) a quantidade de calor transferido
c) a eficiência térmica
d) a pressão média efetiva.
Dados: ; ;
Passo 1
A maior pressão e temperatura do ciclo acontecem no estado 3 (logo após a combustão, o que faz sentido né!? rs).
Como foi dada a temperatura no final da expansão então vamos comparar essa temperatura (estado 4) com a do estado 3, utilizando a relação para isentrópicas.
Antes de achar a pressão em 3 temos de achar a pressão em 2, que também é dada pela relação isentrópica entre 1 e 2.
E a mesma coisa para a temperatura
Passo 2
Utilizando a teoria de gás perfeito vamos fazer a relação “Piviti Povoto”
Como a transformação 2 – 3 é uma iscórica então se reduz a
Passo 3
A quantidade de calor transferido será igual ao calor transferido numa isocórica ou seja:
Como temos todas as temperaturas basta achar a massa e substituir nas equações. A massa pode ser encontrada por meio da equação dos gases perfeitos.
Substituindo
Passo 4
A eficiência térmica de um motor é dada por
Passo 5
A pressão efetiva média é dada por
Como e então
E o trabalho líquido pode ser calculado como
Assim
Resposta
a)
b)
c)
d)
Exercício Resolvido #7
Michael J. Moran, Howard N. Shapiro, Daisied Boettner e Margaret B. Bailey, Princípios de termodinâmica para engenhanaria, Tradução da 7ª ed. americana. Rio de Janeiro: LTC, 2013, pp.453 – Exercício 9.12.
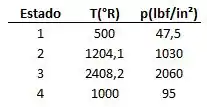
Considere um ciclo de ar-padrão frio Otto. Os dados operacionais são fornecidos em seus estados principais no ciclo, na tabela a seguir. O calor rejeitado pelo ciclo é de 86 Btu/lb de ar (200,0 kJ/kg). Admiitindo e , determine
a) A taxa de compressão.
b) O trabalho líquido por unidade de massa de ar, em Btu/lb.
c) A eficiência térmica.
Passo 1
Olha só que nesse exercício já foram dados todos os estados termodinâmicos, o que vai facilitar bastante nossa vida. A letra a pede a taxa de compressão que é dada pela relação entre o volume antes e depois da comressão:
Se acharmos os volumes e conseguiremos saber a taxa de compressão. Como as pressões de 1 e 2 são conhecidas podemos aplicar a relação de volume e pressão para isentrópicas.
Passo 2
O trabalho líquido por unidade de massa é igual a diferença entre o calor recebido e descartado .
Como o ciclo é Otto, então a troca de calor sempre ocorre a volume constante, portanto, para acharmos e vamos utilizar a seguinte equação.
Perceba que as unidades todas já estão batendo então não é necessário fazer a conversão de unidades.
Passo 3
A eficiência térmica agora é facilmente achada utilizando sua definição
Também poderíamos utilizar a equação com fator de compressão e acharíamos o mesmo valor. Na prova você pode fazer isso para conferir seus resultados =)
Resposta
Exercício Resolvido #8
Michael J. Moran, Howard N. Shapiro, Daisied Boettner e Margaret B. Bailey, Princípios de termodinâmica para engenhanaria, Tradução da 7ª ed. americana. Rio de Janeiro: LTC, 2013, pp.453 – Exercício 9.6.
Um motor de combustão interna de quatro tempos e quatro ciclindros opera a 2800 rpm. Os processos dentro de cada cilindro são modelados como um ciclo de ar-padrão Otto com uma pressão de 101,3 kPa, uma temperatura de 26,7°C, e um volume de 0,00006 m³ no início da compressão. A taxa de compressão é 10, e a pressão máxima no ciclo é de 7446,3 kPa. Determine, utilizando uma análise de ar-padrão frio com , a potência desenvolvida pelo motor. Dado:
Passo 1
Nesse exercício é pedida a potência, por isso vamos ter que calcular o trabalho por unidade de massa , a massa de ar que flui no motor e o tempo de um ciclo. É importante notar também que se trata de um motor de 4 tempos e 4 cilindros.
Primeiro vamos calcular a massa de ar que passa em cada cilindro durante um ciclo. Fazemos isso utilizando os dados do início da compressão: 101,3 kPa de pressão, 26,7°C de temperatura e volume de 0,00006 m³.
Faremos isso utilizando a equação dos gases perfeitos:
Aqui a massa aparece porque estamos utilizando o volume absoluto (em m³) ao invés do volume específico (m³/kg) e também o fato de utilizarmos a constante para o ar (que já leva em consideração o peso molecular do ar), logo a massa é dada por:
Passo 2
Agora precisar achar o trabalho líquido por unidade de massa. Podemos fazer isso achando a diferença entre o trabalho quente e o trabalho frio ou achando o trabalho quente e multiplicando pela eficiência térmica.
Como o fator de compressão já foi dado então vamos calcular a eficiência e multiplicar pelo calor quente.
Passo 3
Agora vamos calcular o calor quente que é dado por:
Porém precisamos das temperaturas nos estados 2 (após a compressão) e 3 (após a combustão). Para achar a temperatura em 2 utilizamos a relação de isentrópicas
E a pressão em 2 é dada por (vamos fazer esse cálculo para poder achar a temperatura em 3)
Já para a temperatura em 3 vamos usar o “Piviti Povoto” para uma isovolumétrica, que se reduz a “PiTi PoTo”
Passo 4
Uhull, depois dessas contas todas vamos calcular o de fato agora
E junto com a eficiência vamos achar o trabalho líquido
Passo 5
Agora estamos na reta final! Repara que o trabalho é representado pela letra minúscula né!? Isso significa que é um trabalho por unidade de massa, para achar o trabalho de fato temos de multiplicar pela massa que foi calculada lá no passo 1.
Como é uma potência tem que aparecer o tempo em algum lugar aí, certo? Ele vem lá da rotação do motor de 2800 rpm e vamos calcular a potência da forma
Vish Maria! Da onde surgiu isso tudo? Calma, vou explicar. O surgiu porque estamos passando de rpm para rotações por segundo, o 4 surgiu porque são 4 cilíndros (e nossa conta é baseada no ciclo de apenas um cilindro, por isso temos de multiplicar pelo número de cilindros) e o ½ surgiu porque é um motor de 4 tempos (ou seja, demora o dobro de tempo que o motor de 2 tempos para fazer o ciclo). No caso do motor de 2 tempos não precisamos multiplicar nem dividir por nenhum valor porque ele faz no tempo certinho.
Voltando