Gás perfeito
Teoria
Fala aí! Hoje nós vamos aprender um pouquinho melhor sobre gás perfeito e a lei dos gases ideais, tá preparado?
Não deixa de conferir também 🧐👇
- Pressão e Volume específicos.
- Relação de Clapeyron.
- Tranformações Gasosas.
- Temperatura, pressão e volume críticos.
O que é um gás ideal?
A ideia de um gás ideal surge da necessidade de se simplificar a análise de gases reais.
Já ouviu aquele clichê de que “ninguém é perfeito”? Também podemos dizê-lo para gases do mundo real, do nosso dia a dia. Quando a gente pensa em um gás real, temos que lembrar que as moléculas que compõem esse fluido sofrem interações intermoleculares, estão em constante colisões umas com as outras, possuem capacidade térmica variável, dentre muitos outros fatores que tornam cálculos envolvendo esses caras extremamente complicados.
E quando falamos de um gás ideal, podemos desconsiderar tudo isso aí! Um gás ideal, ou perfeito, é um fluido idealizado, que tem comportamento e características definidas e simplificadas para facilitar sua análise. Além disso, eles obedecem à lei dos gases ideais e à equação de Clapeyron, como vamos ver logo à frente 😉
Lei dos Gases Ideais
A lei dos gases ideais afirma que a pressão exercida por um gás é proporcional à sua densidade e temperatura. Ela é expressa mais comumente por meio da seguinte equação:
Com:
P
V
n
T
Essa lei dos gases ideais é uma combinação de três leis que vemos melhor em transformações gasosas. Então, na verdade, ela é só mais uma equação de estado. Por conta disso, você pode se deparar com outras formas dessa expressão.
Dá só uma olhada no que acontece se substituirmos aquele n pela razão
Aquele R passa a ser a constante para um gás particular, visto que seu valor passa a depender da massa molar.
Existem outras maneiras de se expressar essa lei dos gases ideais, mas todas elas partem de manipulações a partir dessa que mostrei lá no começo, beleza?
Pressão Reduzida e Temperatura Reduzida
Já que no mundo real não existem gases perfeitos, como eu vou saber se posso usar a lei dos gases ideais?
Um detalhezinho importante é que os gases reais se aproximam dos gases ideais quando submetidos a temperaturas muito altas ou pressões muito baixas! Mas aí surge uma outra questão: quão alta tem que ser essa temperatura e quão baixa tem que ser a pressão?
Pra eliminarmos essa dúvida, introduzimos os conceitos de pressão reduzida
Para sabermos se o gás pode ser considerado perfeito, dividimos os valores de pressão e temperatura reais
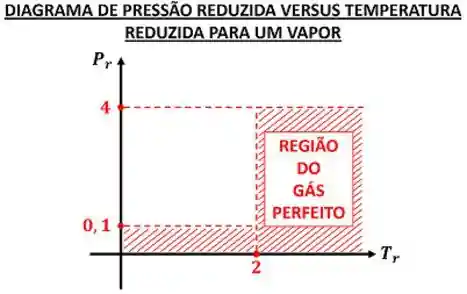
Se a pressão reduzida for próxima de zero, o modelo e a equação de gás perfeito podem ser adotados com boa precisão para qualquer temperatura.
Se a temperatura reduzida for maior que dois, o modelo e a equação de gás perfeito podem ser adotados com boa precisão até pressões reduzidas iguais a quatro.
Dá só uma olhada nesse diagrama que resume tudo isso aí:
Fator de Compressibilidade
O fator de compressibilidade é usado para medir o desvio de comportamento de um gás real em relação ao gás perfeito.
Para uma temperatura fixa, o volume exato de um gás real é diferente do volume previsto pela lei dos gases ideais, concorda? Então, o desvio da idealidade de um gás real pode ser mensurada por meio dessa diferença entre volume verdadeiro e volume previsto para o comportamento como gás ideal, nas mesmas condições de temperatura e pressão.
Esse desvio é expresso por meio do fator de compressibilidade
Quando a substância é considerada um gás perfeito, consegue perceber que o fator de compressibilidade será igual a 1? Afinal, se a lei dos gases ideais diz que
Lei dos Gases Ideais
Pressão Reduzida e Temperatura Reduzida
Fator de Compressibilidade
Exercícios Resolvidos
Exercício Resolvido #1
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 80-2.67
Calcule as constantes de gás ideal do argônio e do hidrogênio utilizando os dados da tabela abaixo.
Passo 1
O enunciado pede que a gente calcule o valor da constante de gás ideal de dois gases: argônio e hidrogênio. Mas o que é essa constante? É um valor que aparece na fórmula de gás ideal!
onde:
- é a pressão absoluta do gás ideal em pascal ;
- é o volume que o gás ocupa em metro cúbico ;
- é a massa do gás em quilograma ;
- é a temperatura do gás em kelvin ;
- é a constante do gás ideal. Ela tem um determinado valor para cada gás. Por exemplo, para o argônio ela tem um valor e para o nitrogênio tem outro. Sua unidade no sistema internacional é .
Ou seja, ela é uma constante que relaciona os valores das propriedades termodinâmicas de um gás. Sua fórmula é:
onde:
- é a constante universal dos gases. Ela tem o mesmo valor para todos os gases. Sua unidade é no Sistema Internacional de Unidades (S.I.). Seu valor é:
- é a massa molar. Sua unidade de acordo com o S.I. é .
O valor da massa molar para o argônio, segundo a tabela dada é:
O valor da massa molar para o hidrogênio, segundo a tabela dada é:
Agora é só substituir esses valores na fórmula da constante para achar as respostas.
Passo 2
Vamos começar a calcular o valor da constante para o argônio :
Para o hidrogênio a fórmula fica:
Pronto! Encontramos o que o problema pedia.
Resposta
Exercício Resolvido #2
Michael A. Boles e Yunus A. Çengel, Thermodynamics: An Engineering Approach, 8ª ed. New York: McGraw-Hill Education, 2015, pp. 156-3.72
Um balão esférico com diâmetro de é preenchido com hélio a e . Determine o número de moles e a massa de hélio no balão. A massa molar do hélio vale .
Passo 1
O exercício pede o número de moles do hélio e a massa desse gás presente no balão . pode ser calculado pela fórmula de gás ideal.
Reorganizando essa fórmula, encontramos uma fórmula para :
onde:
- é a pressão absoluta do gás ideal em pascal . O enunciado diz que a pressão absoluta do gás é:
- é o volume que o gás ocupa em metro cúbico . Essa informação está escondida no enunciado. Ele diz que o balão é esférico com diâmetro de . Isso significa que o seu volume é o volume de uma esfera com esse diâmetro.
- é o número de moles do gás em quilomol ;
- é a temperatura do gás em kelvin . De acordo com enunciado, a temperatura do hélio vale:
- é a constante universal dos gases. Ela tem o mesmo valor para todos os gases. Sua unidade é no Sistema Internacional de Unidades (S.I.). Seu valor é:
Com esses valores calculamos o número de moles do gás , mas ainda falta saber sua massa . A equação da massa é:
é a massa molar. Sua unidade de acordo com o S.I. é . Para o hélio ela vale:
Agora é só começar a substituir os dados para chegar às respostas. Vamos fazer isso no próximo passo!
Passo 2
A fórmula para calcular o número de moles é:
Substituindo esse valor na expressão da massa encontramos:
Acabou! Encontramos os dois resultados!
Resposta
Exercício Resolvido #3
Michael A. Boles e Yunus A. Çengel, Thermodynamics: An Engineering Approach, 8ª ed. New York: McGraw-Hill Education, 2015, pp. 156-3.68
Um tanque rígido de contém de ar a . Determine a leitura de pressão no manômetro, se a pressão atmosférica é . Considere a massa molar do ar igual a .
Passo 1
O exercício pede a pressão do ar lida em um manômetro. Cuidado! Essa pressão não é a pressão absoluta que encontramos na fórmula de gás ideal. A pressão lida no manômetro é a diferença entre a pressão absoluta do gás e a pressão atmosférica. Chamamos essa diferença de pressão manométrica .
onde é a pressão atmosférica. Ela é dada pelo enunciado.
Mas então como podemos calcular a pressão absoluta? A partir da fórmula de gás ideal! É só reorganizar a equação:
onde:
- é a pressão absoluta do gás ideal em pascal ;
- é o volume que o gás ocupa em metro cúbico . A questão dá esse valor em litro :
- é o número de moles do gás em quilomol ;
- é a temperatura do gás em kelvin . De acordo com enunciado, a temperatura do ar vale:
- é a constante universal dos gases. Ela tem o mesmo valor para todos os gases. Sua unidade é no Sistema Internacional de Unidades (S.I.). Seu valor é:
Falta só o número de moles do gás para saber sua pressão absoluta . Ele é obtido através da massa e da massa molar mas ainda falta saber sua massa . A equação da massa é:
O valor de massa molar do ar foi fornecido pelo problema:
A massa do ar também foi dada:
Agora é só começar a substituir os dados para chegar às respostas. Vamos fazer isso no próximo passo!
Passo 2
O número de moles do gás é:
Logo, a pressão absoluta do gás vale:
Enfim podemos calcular a pressão manométrica:
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 80-2.65
Determine a mudança percentual relativa na pressão se dobrarmos a temperatura absoluta de um gás ideal mantendo a massa e o volume constantes. Repita para o caso em que dobramos o valor de e mantemos e constantes.
Passo 1
O enunciado pede para que a gente calcule o valor de duas mudanças relativas.
A primeira é a mudança na pressão absoluta do gás , quando dobramos a sua temperatura absoluta , mantendo a massa do gás e o seu volume constantes. Ou seja a pressão anterior à variação da temperatura é:
Atenção! Como a massa do gás não varia, o número de moles também permanece constante!
é uma constante de valor igual para todos os gases.
A pressão absoluta do gás depois da variação da temperatura fica:
A variação relativa de pressão é calculada a partir da seguinte fórmula:
A explicação da variação relativa de pressão absoluta com a variação do volume ocupado pelo gás é mostrada no próximo passo!
Passo 2
A pressão absoluta do gás antes de variar seu volume é:
Depois que dobramos o valor do volume, sua fórmula vira:
A variação relativa de pressão é calculada a partir da seguinte fórmula:
No passo seguinte nós vamos substituir as fórmulas de pressão nas expressões de variação relativa de pressão.
Passo 3
A variação relativa de pressão, quando dobramos a temperatura absoluta é:
Já para a variação de volume, a variação relativa de pressão fica:
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 81-2.73
Um copo é lavado com água a e é colocado de boca para baixo em uma mesa. O ar ambiente a que foi aprisionado no copo é aquecido até . No processo de aquecimento, ocorrem vazamentos, de modo que, quando a temperatura do ar no copo atinge o valor fornecido, a pressão do ar no copo é acima da pressão ambiente de . Após algum tempo, a temperatura do ar aprisionado no copo volta a ser igual à do ambiente. Determine a pressão no interior do copo, sabendo que a pressão atmosférica é .
Passo 1
O enunciado diz que um copo aprisiona ar dentro dele. Como o copo está mais quente que o ar, o ar é aquecido até atingir uma temperatura de . Quando ele chega nessa temperatura, sua pressão vale acima da pressão atmosférica de . Ou seja, sua pressão vale .
Vamos chamar esse estado, definido por essas duas propriedades, é o estado 1.
Depois, o ar é resfriado junto com o copo, sem vazar, até chegar na temperatura do ambiente . O enunciado pede para calcularmos o valor da pressão depois que o ar é resfriado. Chamamos o estado do ar resfriado de estado 2.
Durante o resfriamento, nosso sistema composto pelo ar continua ocupando o mesmo volume e continua com a mesma quantidade de mol do início do processo de resfriamento. Em outras palavras, o processo ocorre com o valor de volume constante e com o número de mole constante.
Se a gente reorganizar a fórmula de gás ideal, podemos perceber melhor uma dica que vai nos ajudar muito.
O lado direito da segunda equação acima tem valor constante durante todo processo de resfriamento, porque as três variáveis presentes nele são constantes. Como a pressão dividida pela temperatura é igual ao lado direito, seu valor também é constante durante todo o processo.
Por causa disso, descobrimos que:
Se a gente passar a temperatura para o outro lado multiplicando, encontramos a fórmula para calcular .
Pronto, agora que temos a fórmula podemos partir para o cálculo. Essa parte vai ficar no próximo passo de resolução do exercício!
Passo 2
Agora, vamos substituir os valores que conhecemos na fórmula que encontramos:
Pronto! Achamos a resposta!
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 81-2.76
Inicialmente, um tanque rígido, com volume de , contém a e . Suponha que ocorra o vazamento acidental de de para a atmosfera. Sabendo que a temperatura final do no tanque, após o vazamento é , determine a pressão final. Considere a massa molar de igual a .
Passo 1
O sistema termodinâmico desse problema é o nitrogênio presente em um tanque rígido. Antes de ocorrer um vazamento de (estado 1) a pressão no tanque valia e a temperatura do gás valia .
Além disso, o volume ocupado pelo nitrogênio no estado 1 era:
Depois de vazar de (estado 2) o gás ficou com uma temperatura de . A pressão de nesse estado final é a incógnita do problema.
Pode parecer que esses foram os principais dados fornecidos pelo enunciado, mas existe uma informação muito importante escondida nele: como o tanque é rígido, mesmo após o vazamento, seu espaço não mudou. Ou seja, no estado 1 e no estado 2 o gás nitrogênio ocupa o mesmo volume.
Para encontrar a pressão final utilizaremos a equação do gás perfeito reorgazinada.
Só que ainda não sabemos como calcular e .
A fórmula de é:
A massa molar do gás nitrogênio vale:
A massa final do gás está em função da massa antes do vazamento . Logo precisamos saber calcular primeiro. O seu valor é encontrado com a equação de gás perfeito modificada.
Depois de fazer todos esses cálculos teremos condições de descobrir a pressão final no tanque. Mas deixaremos essa etapa pro passo seguinte!
Passo 2
Precisamos começar com o cálculo de .
Com esse valor podemos calcular .
Agora estamos prontos para calcular .
Sabendo isso, chegamos ao cálculo final de .
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 81-2.74
O ar no interior de um motor de combustão interna está a , e ocupa um volume de . A combustão o aquece até , em um processo a volume constante. Qual é a massa de ar e qual é o valor que a pressão atinge nesse processo? Considere a massa molar do ar igual a .
Passo 1
O enunciado fala sobre o ar no interior de um motor de combustão interna. Ele passa por um processo de combustão que faz ele ficar mais quente. Ou seja, o ar tem dois estados: o estado 1 que é o estado antes do aquecimento e o estado 2 que é o estado depois do aquecimento.
Antes do aquecimento (estado 1) o ar tinha a pressão, a temperatura e o volume a seguir:
Uma das incógnitas do enunciado é a massa de ar presente no motor. Já podemos achar uma fórmula para ela a partir desses dados fornecidos pela questão. Pra isso, reorganizamos a fórmula de gás perfeito.
A massa de ar é constante durante todo o processo de aquecimento, porque não tem ar vazando nem ar entrando. Por isso, se calcularmos a massa de ar do estado 1 , já calculamos a massa de ar durante todo o aquecimento. Mas para a gente chegar nesse valor de resta saber uma expressão para .
A massa molar do ar vale:
O exercício também pede para a gente calcular a pressão do ar no estado 2 . Mas vamos deixar essa explicação para o passo seguinte!
Passo 2
A questão fala que o aquecimento ocorre a volume constante. Isso significa que o volume que o ar ocupa no estado 2 é igual ao volume que o ar ocupa no estado 1 .
Além disso, a massa de ar no estado 2 também é igual à massa de ar no estado 1 .
O outro dado sobre o ar no estado 2 informado pelo problema é a temperatura .
Com essas informações, achamos uma expressão par calcular , reorganizando a equação de gás perfeito.
Agora precisamos substituir os dados nas fórmulas encontradas para achar as duas incógnitas. No próximo passo faremos isso!
Passo 3
Primeiro, precisamos calcular o valor do .
Com esse valor, calculamos a massa de ar.
Como a massa de ar permanece constante, descobrimos :
Com essa informação, estamos prontos para achar .
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2013, pp. 80-2.70
Gás hélio armazenado em um tanque de aço de a e é utilizado para encher um balão. Quando a pressão cai para , o fluxo de hélio é interrompido. Se todo o hélio ainda estiver a , qual terá sido o tamanho do balão produzido?
Passo 1
O exercício é pra achar o volume do balão, depois de um tanque cheio de hélio terminar de enchê-lo. Para organizar a solução desse problema, chamaremos de estado 1 o estado em que o tanque está fechado e ainda não encheu o balão.
Nesse estado 1, o enunciado diz que a pressão , a temperatura e o volume do hélio valem:
O balão é enchido de hélio até a pressão do tanque cair para . Isso significa que a pressão no tanque e a pressão no balão se equilibraram. Por isso o hélio do tanque não tem mais força para entrar no balão. O enunciado também diz que o hélio não varia de temperatura durante o processo de enchimento.
Chamamos de estado 2 o estado do hélio depois do enchimento. Nesse momento, o hélio está tanto no tanque quanto no balão. Ou seja, nesse caso, o nosso sistema o nosso sistema é tanto o hélio presente no tanque, quanto o hélio presente no balão. As propriedades do estado 2 informadas na questão foram:
Vamos deixar para o próximo passo as informações do enunciado que estão mais escondidas e precisam de uma interpretação de texto mais cuidadosa!
Passo 2
Como nosso sistema é todo o hélio, ele não varia sua quantidade de moles ao longo do processo de enchimento. Ele muda de lugar, mas sua massa total continua a mesma. Logo:
Podemos achar com a fórmula de gás ideal para o estado 1.
O enunciado quer saber o volume do balão depois do enchimento. Esse volume é igual ao volume do sistema no estado 2 ( é o volume do balão mais volume do tanque) menos o volume do sistema no estado 1 ( é o volume do tanque).
Já sabemos quanto vale , mas quanto vale ? Descobrimos isso, aplicando a fórmula de gás ideal ao estado 2.
Já foi mostrado como calcular todos os valores da equação acima! Então vamos começar nossos cálculos no próximo passo!
Passo 3
Vamos tentar achar primeiro o número de moles de hélio que forma nosso sistema:
Sabemos que o número de moles do sistema não varia do estado 1 para o estado 2.
Agora só falta descobrir o valor do volume no estado 2 para calcular o volume do balão.
O volume do balão é: