Tabelas de Propriedades e Superfícies Termodinâmicas
Teoria
Estado termodinâmico de uma substância pura simples compressível
Vemos através do gráfico -, que precisamos apenas da pressão e do volume específico para determinar a temperatura da água.
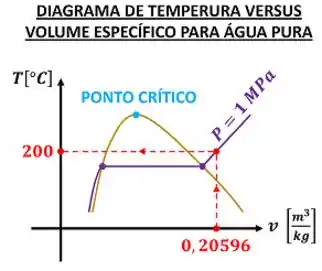
Ou seja, com o valor de apenas duas propriedades intensivas, achamos automaticamente o valor de outra propriedade. Por que isso acontece? Por que não precisamos achar o valor de cada propriedade separadamente? Porque o valor das propriedades intensivas estão conectados entre si por meio de fórmulas!
O exemplo da água ilustra o que acontece com todas as substâncias simples compressíveis: precisamos de apenas duas propriedades intensivas independentes para determinar o valor de todas as outras propriedades e definir um estado termodinâmico. Por causa dessa simplicidade, focaremos nossos estudos exclusivamente nessas substâncias.
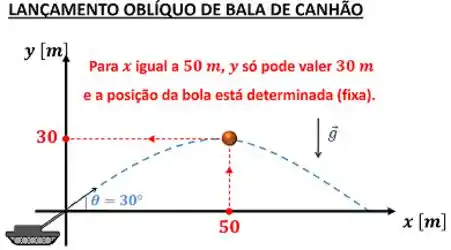
O raciocínio por trás disso, é o mesmo por trás da determinação da posição de uma bala de canhão em lançamento oblíquo. Precisamos de apenas uma coordenada para fixar a posição da bala, porque existe uma relação entre suas posições horizontal e vertical . Da mesma forma, precisamos de apenas duas propriedades independentes para fixar o estado de um sistema, porque existe uma relação entre todas as suas propriedades.
Propriedades intensivas independentes
Mas o que são essas propriedades intensivas independentes que precisam ser determinadas para determinar o estado da substância? Podemos explicar esse conceito com o exemplo da água. Conseguimos determinar seu volume específico , conhecendo apenas sua pressão ?
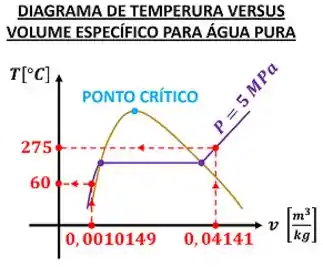
Não, porque o espaço que de água ocupa também depende da sua temperatura ! Isto é, segundo a imagem acima, para um valor de ela pode ter uma infinidade de valores de . Assim como uma formiga andando no chão pode estar em várias coordenadas para uma mesma coordenada , a água pode ter vários volumes específicos para uma mesma pressão.
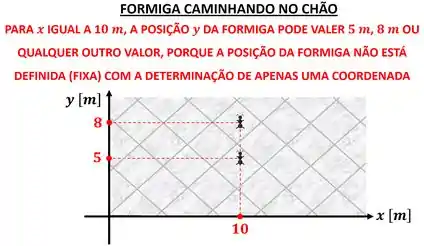
Ou seja, não existe apenas um valor de volume específico para um determinado valor de pressão. Como o valor de volume específico pode ser variado, sem variar o valor da pressão , dizemos que os dois são independentes entre si. Ou melhor, a pressão e o volume específico são duas propriedades intensivas independentes.
Por causa disso, se definirmos os valores de e ao mesmo tempo, conseguimos determinar o estado de uma substância simples compressível, porque o resto das propriedades dependem dessas variáveis independentes por meio de fórmulas.
onde é uma função que calcula o valor da propriedade através dos valores de e .
O caso oposto ocorre entre a pressão de saturação e a temperatura de saturação. Vemos através do gráfico -, que para um valor de pressão de saturação, existe apenas um valor de temperatura de saturação. Não podemos variar um sem variar o outro. Por conta disso, os dois são propriedades dependentes e não são suficientes para determinar um estado.
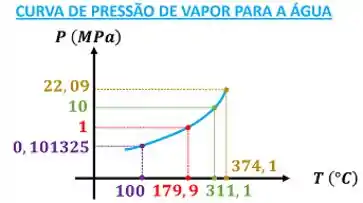
Atenção! Fora da região de saturação, a pressão e a temperatura são propriedades termodinâmicas intensivas independentes. Ou seja, fora da região de saturação, se definirmos seus valores, determinamos o estado da substância.
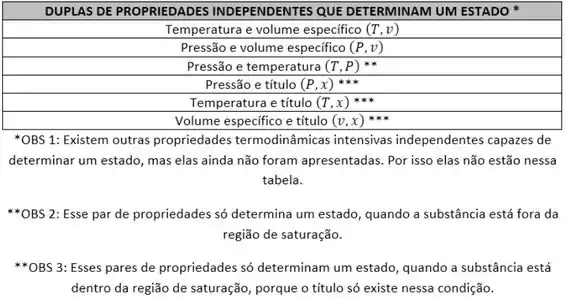
Tabelas de propriedades para líquido comprimido
Foi dito anteriormente, que com apenas duas propriedades intensivas independentes, conseguimos encontrar os valores de todas as outras propriedades intensivas e assim determinar o estado do sistema. Mas como podemos descobrir o valor das propriedades restantes, se não possuímos as fórmulas que as relacionam com as variáveis independentes?
Fazemos isso, usando as tabelas de propriedades! Cada substância tem seu conjunto de tabelas. Existe uma tabela para cada região em que a substância se encontra.
A tabela abaixo apresenta os valores das propriedades da água líquida comprimida. Ela mostra diversos valores de pressão para uma mesma temperatura, porque na região subresfriada, a temperatura e a pressão são propriedades independentes. Além disso, para uma pressão e temperatura, existe apenas um volume específico , pois só existe uma fase (líquido).
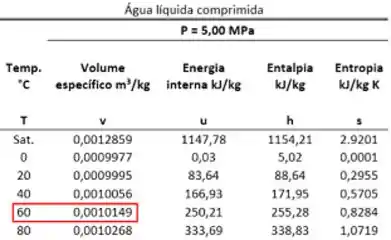
Para exercitar sua utilização, vamos determinar o valor de volume específico para água a e . Nessas condições:
Sua utilização é igual para todas as substâncias. Ou seja, esse exemplo não serve apenas para a água.
Tabelas de propriedades para vapor superaquecido
Ela é muito parecida com a tabela de líquido saturado, porque também possui várias pressões para uma mesma temperatura. Ou seja, nessa região, e permanecem independentes entre si. Como só existe uma fase de vapor nessas condições, para cada par de valor de temperatura e pressão, existe apenas um valor de .
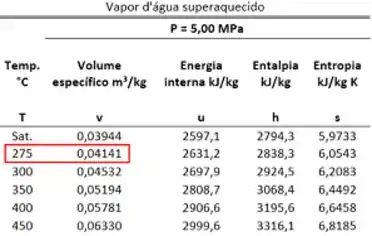
Para praticar seu uso, vamos definir o valor do volume específico da água a e . Neste caso:
Tabelas de propriedades para região de saturação
A tabela abaixo apresenta os valores das propriedades da água, quando ela está na região de vaporização. Ela é diferente das outras duas tabelas, porque para um valor de temperatura, existe apenas um valor de pressão. Essas duas variáveis são dependentes nessa região. Outra diferença é a existência de dois volumes específicos e para um único .
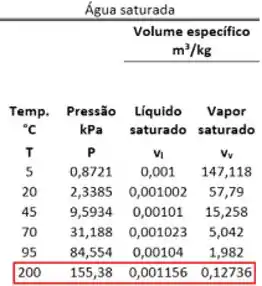
Para exercitar a utilização dessa tabela, vamos encontrar o valor do volume específico da mistura vapor e líquido a e título igual a , sabendo que a fórmula de volume específico médio para misturas bifásicas entre líquido e vapor é:
onde:
- é o volume específico do líquido saturado
- é o volume específico do vapor saturado
- é a massa do líquido saturado
- é a massa do vapor saturado
- é a massa total da mistura bifásica
Ou seja, a tabela de saturação possui dois valores de , porque existe um valor para cada fase.
Sabendo que a equação do título é:
E que a fração de líquido saturado é:
Encontramos:
Descobrimos pela tabela que o volume específico do líquido saturado a vale e o volume específico do vapor saturado a vale . Substituindo na expressão:
Em algumas tabelas, existe uma variável . Ela é a diferença entre o volume específico do vapor saturado e o volume específico do líquido saturado da substância para uma temperatura de saturação.
Para o exercício proposto vale:
Além das três tabelas mostradas, existem as tabelas de: sublimação (mistura de sólido com vapor), fusão (mistura de sólido com líquido) e sólido comprimido. No entanto, elas são mais incomuns de cair em questões de prova.
Superfície termodinâmica
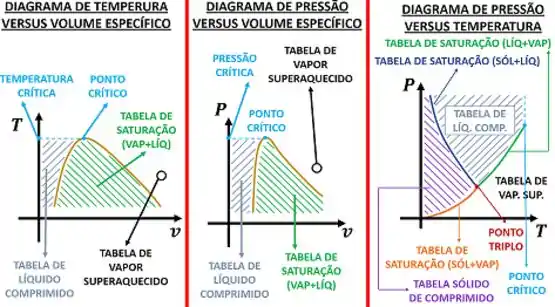
Para cada par de valores de volume específico e temperatura, existe apenas um valor de pressão que uma determinada substância pode assumir. Isso fica mais claro, desenhando curvas de mesma temperatura em um diagrama -. Se quisermos determinar a pressão para outros valores de temperatura, teríamos que desenhar outras curvas de temperaturas iguais.
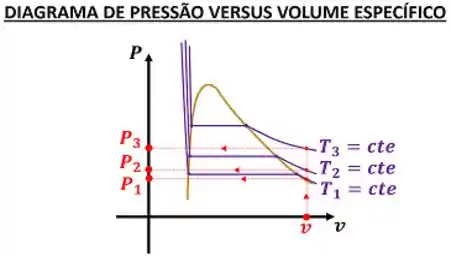
Como uma substância pode variar sua temperatura por uma infinidade de valores, desenhar várias curvas de constante em um mesmo plano - dificultaria a visualização dos valores de pressão correspondentes. Então como podemos obter uma informação gráfica sem usar um diagrama bidimensional poluído? Através da superfície termodinâmica!
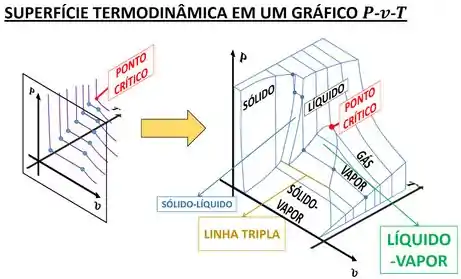
Ela é formada pelo conjunto de curvas de temperaturas constantes colocadas umas atrás da outra. Assim se constrói um gráfico --. Cada ponto sobre essa superfície representa um estado termodinâmico que uma substância pode assumir.
Propriedades intensivas independentes
Tabelas de propriedades para líquido comprimido
Tabelas de propriedades para vapor superaquecido
Tabelas de propriedades para região de saturação
Superfície termodinâmica
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine se a água é um vapor superaquecido, um líquido comprimido ou se ela está saturada, usando a tabela de propriedades dada. Considere o seguinte caso:
,
Passo 1
Para saber se a água está em uma dessas três opções. Devemos comparar sua pressão com a pressão de saturação ou devemos comparar sua temperatura com a temperatura de saturação.
Caso ela tenha pressão menor que a pressão de saturação ou temperatura maior que a temperatura de saturação, ela é um vapor superaquecido!
Caso ela tenha pressão e temperatura iguais à pressão e à temperatura de saturação, ela estará saturada.
Caso ela tenha pressão maior que a pressão de saturação ou temperatura menor que a temperatura de saturação, ela é um líquido comprimido!
O enunciado informa que:
Então agora vamos comparar esses valores com as condições de saturação da água informadas pela tabela!
Passo 2
Vemos que para a temperatura de saturação da água vale . Ou seja:
Comparando a temperatura da água com a sua temperatura de saturação, vemos que:
Logo a água é um líquido comprimido.
Resposta
A água é um líquido comprimido.
Exercício Resolvido #2
Elaboração própria
Determine se a água é um vapor superaquecido, um líquido comprimido, um sólido comprimido ou se ela está saturada, usando a tabela de propriedades dada. Considere que a temperatura da água seja de , que a sua pressão manométrica seja e que a água congela a nessa pressão.
Passo 1
Para saber se a água está em uma dessas quatro opções, devemos comparar sua temperatura com a temperatura de saturação.
Caso ela tenha temperatura maior que a temperatura de saturação, ela é um vapor superaquecido!
Caso ela tenha temperatura à temperatura de saturação, ela estará saturada.
Caso ela tenha temperatura menor que a temperatura de saturação, ela é um líquido comprimido ou um sólido comprimido!
Para saber em qual das duas fases a água está, basta comparar a sua temperatura com a temperatura de congelamento da água. Se sua temperatura for menor que a temperatura de congelamento, ela é um sólido comprimido.
Se sua temperatura é maior que a temperatura de fusão, ela é um líquido comprimido.
O enunciado informa que:
Mas ele também diz que a sua pressão manométrica vale . Isso significa que a água está em vácuo absoluto? Não! A pressão manométrica é a diferença entre o valor da pressão e a pressão atmosférica.
Então a pressão da água vale:
Então agora vamos comparar esses valores com as condições de saturação da água informadas pela tabela e com a temperatura de fusão dada!
Passo 2
Vemos que para a temperatura de saturação da água vale . Ou seja:
Comparando a temperatura da água com a sua temperatura de saturação, vemos que:
Logo a água é um líquido comprimido ou um sólido comprimido. Para saber, temos que comparar sua temperatura com a temperatura de fusão. Vamos deixar isso para o próximo passo!
Passo 3
A temperatura de fusão foi unformada pelo enunciado e vale .
Comparando esse valor com a temperatura da água , vemos que:
Por causa disso, a água é um sólido comprimido!
Resposta
A água é um sólido comprimido.
Exercício Resolvido #3
Elaboração própria
Determine a temperatura de saturação da água, usando a tabela de propriedades dada. Considere que a pressão da água seja de .
Passo 1
A tabela do enunciado informa as temperaturas de saturação para diversos valores de pressão. O problema é que nenhum desses valores de pressão é igual ao valor de pressão da água! E aí, como resolveremos isso?
Interpolando o valor de temperatura de saturação! E como fazemos isso? Considerando que a temperatura de saturação varia linearmente com a pressão para pressões intermediárias que não existem na tabela. Ou seja:
Ou seja, determinamos uma temperatura que está no meio de outros dois valores de temperatura informados pela tabela, calculando a equação da reta que liga a menor pressão do intervalo com a maior pressão do intervalo.
No caso estudado, a pressão da água vale . Por causa disso, ela está no meio do intervalo entre a pressão menor de e a pressão maior de .
Sabendo disso, precisamos encontrar a equação da reta que liga esses dois pontos! Esse é o nosso próximo passo!
Passo 2
A equação da reta tem duas formas:
Ou:
Visualizamos essa informação através da imagem abaixo:
Para o nosso caso a variável é a nossa pressão e a variável dependente é a temperatura de saturação, porque é sempre o valor da propriedade que queremos interpolar. Logo:
é o valor da pressão para a qual queremos encontrar a temperatura de saturação.
é o valor inferior do intervalo. Ele é o valor inferior de pressão do intervalo.
é o valor superior do intervalo. Ele é o valor superior de pressão do intervalo.
é o valor interpolado da temperatura de saturação.
é o valor da propriedade que queremos encontrar relativo ao valor inferior de pressão. Ele é o valor da temperatura de saturação para a pressão inferior.
é o valor da propriedade que queremos encontrar relativo ao valor superior de pressão. Ele é o valor da temperatura de saturação para a pressão superior.
No próximo passo substituiremos todos esses valores na fórmula da reta.
Passo 3
Pronto, achamos o valor interpolado de temperatura de saturação!
Resposta
Exercício Resolvido #4
Elaboração própria
Determine se a água é um vapor superaquecido, um líquido comprimido ou se ela está saturada, usando a tabela de propriedades dada. Além disso, determine se a água está na região de saturação, na região de vapor superaquecido ou na região de líquido comprimido, localizando o seu estado nos gráficos -, - e -. Considere que a temperatura da água seja de e a sua pressão seja de .
Passo 1
Para saber se a água está em uma dessas três opções, devemos comparar sua pressão com a pressão de saturação ou devemos comparar sua temperatura com a temperatura de saturação.
Caso ela tenha pressão menor que a pressão de saturação ou temperatura maior que a temperatura de saturação, ela é um vapor superaquecido!
Caso ela tenha pressão e temperatura iguais à pressão e à temperatura de saturação, ela estará saturada.
Caso ela tenha pressão maior que a pressão de saturação ou temperatura menor que a temperatura de saturação, ela é um líquido comprimido!
O enunciado informa que:
Então agora vamos comparar esses valores com as condições de saturação da água informadas pela tabela! Opa! Tem um problema! A tabela do enunciado informa as pressões de saturação para diversos valores de temperatura. O problema é que nenhum desses valores de temperatura é igual ao valor de temperatura da água! Resolveremos isso no próximo passo!
Passo 2
Achamos a pressão de saturação para a temperatura certa, calculando essa propriedade através da interpolação! E como fazemos isso? Considerando que a pressão de saturação varia linearmente com a temperatura para temperaturas intermediárias que não existem na tabela. Ou seja:
Determinamos uma pressão que está no meio de outros dois valores de pressão informados pela tabela, calculando a equação da reta que liga a menor temperatura do intervalo com a maior temperatura do intervalo .
No caso estudado, a temperatura da água vale . Por causa disso, ela está no meio do intervalo entre a temperatura menor de e a temperatura maior de .
Sabendo disso, precisamos encontrar a equação da reta que liga esses dois pontos!
Fica faltando saber qual é a região que o estado da água está. Descobrimos isso, olhando para os diagramas de fase.
Se a água for vapor superaquecido, o estado dela estará dentro da região de vapor superaquecido. Se a água for líquido comprimido, o estado dela estará dentro da região de líquido comprimido. E se a água estiver saturada, o estado dela estará dentro da região de saturação!
Agora vamos aprender a interpolar!
Passo 3
A equação da reta tem duas formas:
Ou:
Visualizamos essa informação através da imagem abaixo:
Para o nosso caso a variável é a nossa tempertura e a variável dependente é a pressão de saturação, porque é sempre o valor da propriedade que queremos interpolar. Logo:
é o valor da temperatura para a qual queremos encontrar a pressão de saturação.
é o valor inferior do intervalo. Ele é o valor inferior de temperatura do intervalo.
é o valor superior do intervalo. Ele é o valor superior de temperatura do intervalo.
é o valor interpolado da pressão de saturação.
é o valor da propriedade que queremos encontrar relativo ao valor inferior de temperatura. Ele é o valor da pressão de saturação para a temperatura inferior.
é o valor da propriedade que queremos encontrar relativo ao valor superior de temperatura. Ele é o valor da pressão de saturação para a temperatura superior.
No próximo passo substituiremos todos esses valores na fórmula da reta.
Passo 4
Pronto, achamos o valor interpolado de pressão de saturação! Na próxima etapa, a gente vai comparar esse valor com a pressão da água informada pelo enunciado.
Passo 5
Vemos que para a pressão de saturação da água vale . Ou seja:
Comparando a pressão da água com a sua pressão de saturação, vemos que:
Logo a água é um vapor superaquecido. Por causa disso, o estado da água está em algum ponto da região de vapor superaquecido (região branca dos gráficos).
Resposta
A água é vapor superaquecido e, por isso, pertence à região de vapor superaquecido dos diagramas.
Exercício Resolvido #5
Elaboração própria
Determine se a água é um vapor superaquecido, um líquido comprimido ou se ela está saturada, usando a tabela de propriedades dada. Além disso, determine se a água está na região de saturação, na região de vapor superaquecido ou na região de líquido comprimido, localizando o seu estado na superfície termodinâmica. Considere que a temperatura da água seja de e a sua pressão seja .
Passo 1
Para saber se a água está em uma dessas três opções, devemos comparar sua pressão com a pressão de saturação.
Caso ela tenha pressão menor que a pressão de saturação, ela é um vapor superaquecido!
Caso ela tenha pressão igual à pressão de saturação, ela estará saturada.
Caso ela tenha pressão maior que a pressão de saturação, ela é um líquido comprimido!
O enunciado informa que:
Então agora vamos comparar esses valores com as condições de saturação da água informadas pela tabela! Mas não podemos fazer isso agora! A tabela do enunciado informa as pressões de saturação para diversos valores de temperatura. O problema é que nenhum desses valores de temperatura é igual ao valor de temperatura da água! Resolveremos isso no próximo passo!
Passo 2
Achamos o valor de pressão de saturação para a temperatura certa, calculando seu valo através da interpolação! E como fazemos isso? Considerando que a pressão de saturação saturado varia linearmente com a temperatura para temperaturas intermediárias que não existem na tabela. Ou seja:
Determinamos uma pressão que está no meio de outros dois valores de pressão informados pela tabela, calculando a equação da reta que liga a menor temperatura do intervalo com a maior temperatura do intervalo .
No caso estudado, a temperatura da água vale . Por causa disso, ela está no meio do intervalo entre a temperatura menor de e a temperatura maior de .
Sabendo disso, precisamos encontrar a equação da reta que liga esses dois pontos!
Fica faltando saber qual é a região que o estado da água está. Descobrimos isso, olhando para a superfície termodinâmica.
Cada região tem uma cor. Se a água for vapor superaquecido, o estado dela estará dentro da região azul. Se a água for líquido comprimido, o estado dela estará dentro da região vermelha. E se a água estiver saturada, o estado dela estará dentro da região verde!
Agora vamos aprender a interpolar!
Passo 3
A equação da reta tem duas formas:
Ou:
Visualizamos essa informação através da imagem abaixo:
Para o nosso caso a variável é a nossa tempertura e a variável dependente é a pressão de saturação, porque é sempre o valor da propriedade que queremos interpolar. Logo:
é o valor da temperatura para a qual queremos encontrar a pressão de saturação.
é o valor inferior do intervalo. Ele é o valor inferior de temperatura do intervalo.
é o valor superior do intervalo. Ele é o valor superior de temperatura do intervalo.
é o valor interpolado da pressão de saturação.
é o valor da propriedade que queremos encontrar relativo ao valor inferior de temperatura. Ele é o valor da pressão de saturação para a temperatura inferior.
é o valor da propriedade que queremos encontrar relativo ao valor superior de temperatura. Ele é o valor da pressão de saturação para a temperatura superior.
No próximo passo substituiremos todos esses valores na fórmula da reta.
Passo 4
Pronto, achamos o valor interpolado de pressão de saturação! Na próxima etapa, a gente vai comparar esse valor com a pressão da água informada pelo enunciado.
Passo 5
Vemos que para a pressão de saturação da água vale . Ou seja:
Comparando a pressão da água com a sua pressão de saturação, vemos que:
Logo a água é um vapor superaquecido. Por causa disso, o estado da água está em algum ponto da região azul da superfície termodinâmica.
Resposta
A água é um vapor superaquecido e está na região azul da superfície termodinâmica.
Exercício Resolvido #6
Elaboração própria
Determine se a água é um vapor superaquecido, um líquido comprimido ou se ela está saturada, usando a tabela de propriedades dada. Considere que a temperatura da água seja de e o seu volume específico seja .
Passo 1
Para saber se a água está em uma dessas três opções, devemos comparar seu volume específico com os volumes específicos de vapor saturado e de líquido saturado .
Caso ela tenha volume específico menor que o volume específico de líquido saturado, ela é um líquido comprimido.
Caso ela tenha volume específico maior que o volume específico do vapor saturado, ela é um vapor superaquecido.
Caso ela tenha volume específico entre os valores de volume específico para o líquido saturado e para o vapor superaquecido, ela está saturada.
O enunciado informa que:
Então agora vamos comparar esses valores com as condições de saturação da água informadas pela tabela!
Opa! Não vai dar! A tabela do enunciado informa não informa os valores de volume específico ( e ) para o valor de temperatura da água. A solução disso está no próximo passo!
Passo 2
Achamos os volumes específicos de vapor saturado e líquido saturado para a temperatura certa, calculando essas propriedades através da interpolação! E como fazemos isso? Considerando que o volume específico saturado varia linearmente com a temperatura para temperaturas intermediárias que não existem na tabela.
Ou seja, determinamos um volume específico está no meio de outros dois valores informados pela tabela, calculando a equação da reta que liga a menor temperatura do intervalo com a maior temperatura do intervalo .
No caso estudado, a temperatura da água vale . Por causa disso, o ponto que queremos está no meio do intervalo entre a temperatura menor de e a temperatura maior de .
Sabendo disso, precisamos encontrar a equação da reta que liga esses dois pontos!
Agora vamos aprender a interpolar!
Passo 3
A equação da reta tem duas formas:
Ou:
Visualizamos essa informação através da imagem abaixo:
Vamos encontrar uma equação da reta para cada volume específico: uma para o volume específico do líquido saturado e outra para o volume específico do vapor saturado.
Vamos começar com o líquido saturado. Para esse caso, a variável é a nossa tempertura e a variável dependente é o volume específico do líquido saturado, porque é sempre o valor da propriedade que queremos interpolar. Logo:
é o valor da temperatura para a qual queremos encontrar o volume específico do líquido saturado.
é o valor inferior do intervalo. Ele é o valor inferior de temperatura do intervalo.
é o valor superior do intervalo. Ele é o valor superior de temperatura do intervalo.
é o valor interpolado do volume específico do líquido saturado.
é o valor da propriedade que queremos encontrar relativo ao valor inferior de temperatura. Ele é o valor do volume específico do líquido saturado para a temperatura inferior.
é o valor da propriedade que queremos encontrar relativo ao valor superior de temperatura. Ele é o valor do volume específico do líquido saturado para a temperatura superior.
No próximo passo substituiremos todos esses valores na fórmula da reta que encontramos!
Passo 4
Pronto, achamos o valor interpolado de volume específico do líquido saturado!
Passo 5
Agora só falta encontrar a equação da reta para cada volume específico do vapor saturado para poder descobrir a fase da água. Para esse caso, a variável é a nossa tempertura e a variável dependente é o volume específico do vapor saturado, porque é sempre o valor da propriedade que queremos interpolar. Logo:
é o valor da temperatura para a qual queremos encontrar o volume específico do vapor saturado.
é o valor inferior do intervalo. Ele é o valor inferior de temperatura do intervalo.
é o valor superior do intervalo. Ele é o valor superior de temperatura do intervalo.
é o valor interpolado do volume específico do vapor saturado.
é o valor da propriedade que queremos encontrar relativo ao valor inferior de temperatura. Ele é o valor do volume específico do vapor saturado para a temperatura inferior.
é o valor da propriedade que queremos encontrar relativo ao valor superior de temperatura. Ele é o valor do volume específico do vapor saturado para a temperatura superior.
No próximo passo a gente vai substituir todos esses valores na fórmula da reta que encontramos!
Passo 6
Encontramos o valor interpolado de volume específico do vapor saturado! Na próxima etapa, a gente vai comparar todos os valores de volume específico (, e ).
Passo 7
Vemos que para os volumes específicos são:
Comparando o volume específico da água com esses valores, vemos que:
Como:
a água é um líquido saturado. Ou seja, ela está saturada.
Resposta
A água está saturada.
Exercício Resolvido #7
Elaboração própria
Qual é o volume específico da mistura saturada de água líquida com vapor d’água a com um título de ? Use a tabela de propriedades abaixo.
Passo 1
O enunciado pede que a gente calcule o volume específico médio da mistura bifásica . Precisamos descobrir esse valor através das duas propriedades dadas:
é o título da água. Ou seja, é a porcentagem de massa da mistura que é vapor.
é a temperatura da mistura.
A fórmula de volume específico médio em função do título é:
onde:
- é o volume específico do líquido saturado presente na mistura. Seu valor depende da temperatura . Descobrimos seu valor através da tabela;
- é o volume específico do vapor saturado presente na mistura. Seu valor depende da temperatura . Descobrimos seu valor através da tabela;
Falta saber quanto valem os volumes específicos das fases saturadas, mas a tabela não tem esses valores para a temperatura de . Ou seja, precisamos interpolar essas duas propriedades para descobrí-los. Entenderemos isso na próxima etapa!
Passo 2
Para interpolar, vamos considerar que os volumes específicos saturados variam linearmente entre uma temperatura da tabela e outra temperatura vizinha da tabela. Por causa dessa aproximação, os volumes específicos serão obtidos a partir da equação da reta que passa pelos dois pontos mais próximos de . No ponto 1 da reta, a temperatura é:
Além disso, seus volumes específicos saturados são:
No ponto 2 da reta, temos:
Além disso, seus volumes específicos saturados são:
Como uma reta é definida por dois pontos diferentes, a equação das duas retas que calculam os volumes específicos já está definida:
Substituindo os valores mostrados de , , , , , e nas fórmulas, achamos os volumes específicos finais. Com essas propriedades, achamos o volume específico médio pela fórmula dele. Então vamos começar a substituir os dados! É isso que faremos na próxima etapa!
Passo 3
Começando pelo volume específico do líquido saturado:
Para o volume específico do vapor saturado, temos:
Agora usaremos esses resultados na expressão de volume específico médio para chegar na resposta final.
Tá vendo? O que é bom acaba rápido! Já terminamos o exercício! ;-)
Resposta
Exercício Resolvido #8
Elaboração própria
Qual é o título da mistura saturada de água líquida com vapor d’água a ? Considere que o volume específico médio da mistura vale . Use a tabela de propriedades abaixo.
Passo 1
O enunciado pede que a gente calcule o título da mistura bifásica . Precisamos descobrir esse valor através das duas propriedades dadas:
é volume específico médio da mistura bifásica.
é a temperatura da mistura.
A fórmula do título em função do volume específico médio é:
onde:
- é o volume específico do líquido saturado presente na mistura. Seu valor depende da temperatura . Descobrimos seu valor através da tabela;
- é o volume específico do vapor saturado presente na mistura. Seu valor depende da temperatura . Descobrimos seu valor através da tabela;
Falta saber quanto valem os volumes específicos das fases saturadas, mas a tabela não tem esses valores para a temperatura de . Ou seja, precisamos interpolar essas duas propriedades para descobrí-los. Entenderemos isso na próxima etapa!
Passo 2
Para interpolar, vamos considerar que os volumes específicos saturados variam linearmente entre uma temperatura da tabela e outra temperatura vizinha da tabela. Por causa dessa aproximação, os volumes específicos serão obtidos a partir da equação da reta que passa pelos dois pontos mais próximos de . No ponto 1 da reta, a temperatura é:
Além disso, seus volumes específicos saturados são:
No ponto 2 da reta, temos:
Além disso, seus volumes específicos saturados são:
Como uma reta é definida por dois pontos diferentes, a equação das duas retas que calculam os volumes específicos já está definida:
Substituindo os valores mostrados de , , , , , , e nas fórmulas, achamos os volumes específicos finais. Com essas propriedades, achamos o título pela fórmula dele. Então vamos começar a substituir os dados! É isso que faremos na próxima etapa!
Passo 3
Começando pelo volume específico do líquido saturado:
Para o volume específico do vapor saturado, temos:
Agora usaremos esses resultados na expressão de volume específico médio para chegar na resposta final.
Prontinho! Terminamos mais um exercício!