Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 106
106- Um conjunto cilindro-pistão contém, inicialmente, refrigerante a e título . O pistão apresenta área da seção transversal igual a , massa de e está travado por um pino. O pino é, então, removido e espera-se que o sistema atinja o equilíbrio. Sabendo que a pressão atmosférica é e que a temperatura no estado final é igual a , determine
- A pressão e o volume no estado final
- O trabalho realizado pelo
Passo 1
Agora começa a seção das perguntas mais interessantes, digamos assim onde temos que ter um raciocínio um pouco mais elaborado sobre o que queremos fazer.
E vou te falar que essa não foi uma boa primeira impressão pois se liga na versão original dessa questão
Tá dizendo que o volume inicial é de coisa que no livro em português está faltando. Sem esse dado não tem como resolver a questão. Aiaiaiaiai pra equipe que traduziu o livro. (a massa também está diferente, mas vamos fazer aqui como mesmo)
Inicialmente vamos ver como se comporta as pressões nesse sistema quando o pino é solto
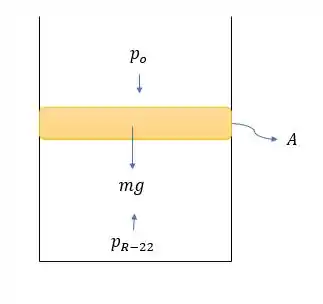
De certa forma a pressão do líquido refrigerante segura a pressão atmosférica e a pressão da área do disco que é dando o seguinte equilíbrio
Então como , então:
Como e ; , então:
E essa é a pressão que é exercida desde o estado inicial até o estado final da expansão do líquido e que responde uma parte da letra
Passo 2
A letra é que é mais interessante, primeiramente vamos anotar os dados que a questão nos dá para o (no meio do caminho resolveremos o volume final, tenha fé)
Inicialmente:
Pela tabela no anexo do livro da sexta edição:
Então o volume específico da substância será:
Pois temos um título de e ela é usada aqui.
Então a massa total do líquido refrigerante será:
Já que o volume inicial é de como a questão traduzida nos fez o favor de não nos informar
E como a massa não é jogada fora e a temperatura no estado final é de e a pressão é de então pela tabela teremos um volume específico de:
O que nos dá um volume final de:
Passo 3
Então o trabalho total do sistema é de:
Já que ele é realizado a pressão constante (de