Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 113
Vapor de água a e entra em uma turbina adiabática de dois estágios a uma vazão de . Extraem-se do vapor ao final do primeiro estágio a uma pressão de , para uma outra finalidade. O restante do vapor de água é expandido no segundo estágio e deixa a turbina a . Considerando que a turbina tem uma eficiência isentrópica de determine o potencial de trabalho desperdiçado durante esse processo como resultado das irreversibilidades. Considere que a vizinhança está a .
Passo 1
Vamos lá, estudantes! O vapor se expande em uma turbina adiabática de dois estágios, de um estado especificado para uma pressão especificada. Algum vapor é extraído no final do primeiro estágio. O potencial de energia desperdiçada deve ser determinado. O potencial de trabalho desperdiçado é equivalente à exergia destruída durante um processo, que pode ser determinada a partir de um equilíbrio de exergia ou diretamente de sua definição.
Passo 2
A taxa total de geração de entropia durante este processo é determinada tomando a turbina inteira, que é um volume de controle, como o sistema e aplicando o equilíbrio de entropia. Observando que este é um processo de fluxo constante e que não há transferência de calor,
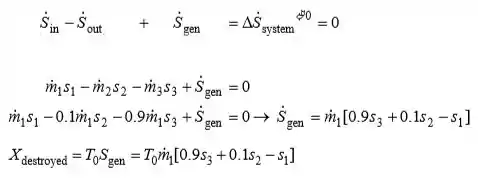
Das mesas de vapor (Tabelas A-4 a 6),
E,
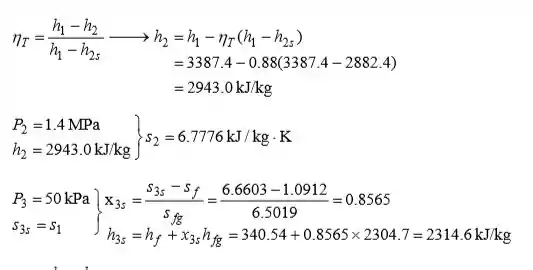
E,
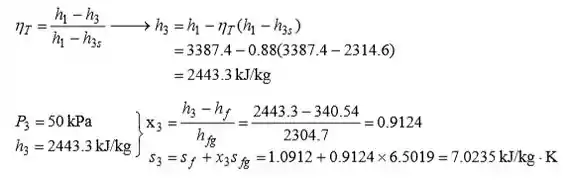
Passo 3
Substituindo, o potencial de trabalho desperdiçado está determinado a ser
