Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 109
Uma turbina a vapor está equipada para “sangrar” do vapor de entrada para aquecimento de água de alimentação. Ela é operada com vapor a e na entrada, uma pressão de “sangramento” de e uma pressão de escape de . O rendimento da turbina entre a entrada e o ponto de “sangria” é de e a eficiência entre o ponto de “sangria” e de escape é de . Calcule a eficiência de segunda lei dessa turbina. Considere .
Passo 1
Vamos lá, estudantes! O vapor é acelerado em um bocal. O vapor é expandido em uma turbina de dois estágios. Seis por cento do vapor de entrada é sangrado para o aquecimento da água de alimentação. As eficiências isentrópicas para os dois estágios da turbina são dadas. A eficiência da segunda lei da turbina deve ser determinada.
Passo 2
Há uma entrada e duas saídas. Nós tomamos a turbina como o sistema, que é um volume de controle desde que a massa atravessa o limite. O balanço energético para este sistema de fluxo constante pode ser expresso na forma de taxa como
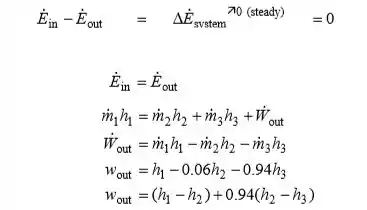
As entalpias isentrópicas e reais em três estados são determinadas usando tabelas de vapor como se segue:
Passo 3
Substituindo no balanço energético por unidade de fluxo de massa na entrada da turbina, obtemos,
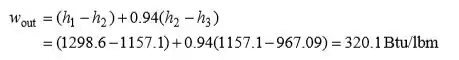
A saída de trabalho reversível por unidade de fluxo de massa na entrada da turbina é,
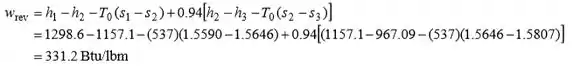
A eficiência da segunda lei é então
