Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 111
111- Um arranjo cilindro-pistão contém de água. Inicialmente, o volume interno é igual a e a temperatura de água é .
A água é então comprimida num processo quase-estático e isotérmico até que o título se torne igual a . Calcule o trabalho envolvido no processo. Admita que o vapor d’água se comporta como um gás perfeito durante todo o processo.
Passo 1
Então galera, já sabem do esquema né, vamos ver como essa água está no estado inicial
Já temos um bom norte por aqui, pois o volume específico no estado inicial será de:
O que é bastante coisa! O que certamente nos diz que temos um gás aqui.
O que também conseguimos calcular aqui no estado inicial é a pressão já que pela tabela a pressão de saturação é de e já que temos uma transformação isotérmica a transformação sai de um vapor e com certeza passa pelo ponto de saturação na mesma temperatura ou seja:
Ou:
Então a pressão em será (para e pela tabela )
Explicando pelo gráfico o que fizemos nós teremos algo como:
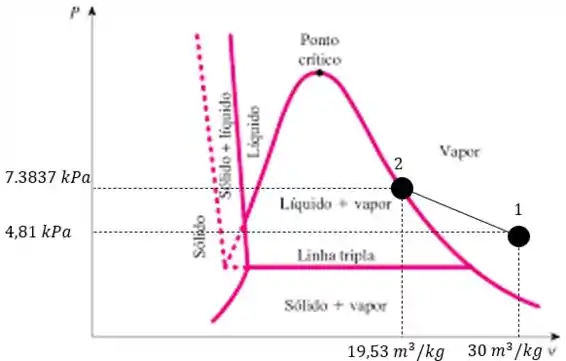
Então o trabalho nesse trecho será de:
Já que o volume específico diminui então o trabalho é negativo.
Passo 2
Agora no estado essa água é comprimida até ter o título de , e mantendo a mesma temperatura e pela tabela teremos
Então o volume específico com a titulação a será de:
E para se manter a mesma temperatura em um estado de líquido e vapor com saturação a pressão no estado deve se manter a (esse estado é o que tem titulação de )
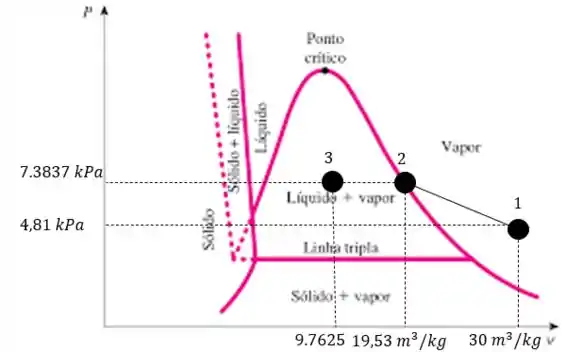
Então o volume nesse estado será de
E o trabalho no processo de para será de:
Já que a pressão é constante
Então o trabalho total será de:
E o processo foi esse, até mais tardeeeee!