113- Um conjunto cilindro-pistão-mola contém, inicialmente, de refrigerante a e título de . O conjunto é aquecido e não se restringe o movimento do pistão.
Nota-se que a última gota de refrigerante desaparece quando a temperatura atinge . O aquecimento é interrompido quando a temperatura atinge .
Determine a pressão no estado final e o trabalho realizado no processo. Observe que será necessário um procedimento iterativo para determinar a pressão final. Utilize o valor de como estimativa inicial para o cálculo da pressão.
Passo 1
Vocês prontos alunos?
ESTAMOS PROFESSOR!
Eu não ouvi direito!
ESTAMOS PROFESSOR
OOOOOOO vive num abacaxi e mora no mar
Pera, errei, vamos para mais uma questão de termodinâmica rapaziada :D
Vamos anotar o estado inicial da água nesse instante, já que dominar os estados é o papel de um verdadeiro avatar (estou inspirado nas referências hoje, apesar que são os 4 elementos e não os estados, mas vocês pegaram)
Dessa forma o estado inicial é dado por:
Como as propriedades do líquido não pressurizado está na tabela então vamos correndo para lá pegar as propriedades mais importantes quando
Isso nos dá um volume específico no momento inicial de:
Outra coisa importante para descobrirmos é a massa desse líquido no conjunto e isso é encontrado por:
Então nós temos desse líquido em todo o processo
Passo 2
E aí temos o estado que será onde? Em , melhor não, pois atente-se a informação
Nota-se que a última gota de refrigerante desaparece quando a temperatura atinge
A informação dada aqui é que o líquido deixa de estar no estado (saturado-vapor) para ser totalmente vapor, com , então esse é o segundo estado.
E nesse estado pela tabela
Pois lembre-se aqui o líquido virou vapor (totalmente)
Não precisamos muito nos preocupar com o volume aqui pois o trabalho ocorre entre os estados iniciais e os finais, e aqui é um estado intermediário
E não temos muito mais a se falar nesse estado
Passo 3
Aí agora podemos falar do estado quando que seria o terceiro estado desse líquido, e nossa tabela não chega a essa temperatura tão elevada, temos que usar a tabela para essa missão.
E usando a estimativa que o enunciado nos dá de essa pressão nesse estado ser próxima de , então pela tabela as propriedades desse líquido a e a essa temperatura são de:
![]()
Então considerando que a pressão no terceiro segue a mesma proporção do primeiro estado para o segundo estado, ou seja, a variação da pressão é linear e segue a mesma reta que:
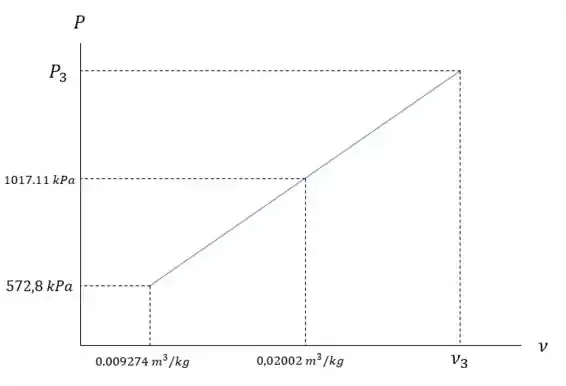
Então a pressão equivale a seguinte expressão:
Qualquer semelhança com uma equação da reta é por que é isso mesmo.
E assim correlacionamos com ao substituirmos os valores que conhecemos:
Passo 4
E essa reta tem que coincidir com a reta que temos entre a pressão de e de para vapor saturado, o que significa:
Você tem que entender que essas retas são aproximações que temos que tomar, para termos a estimativa do estado final
O que nos dá uma equação de:
Fazendo um sistema com as duas equações temos as duas retas abaixo:
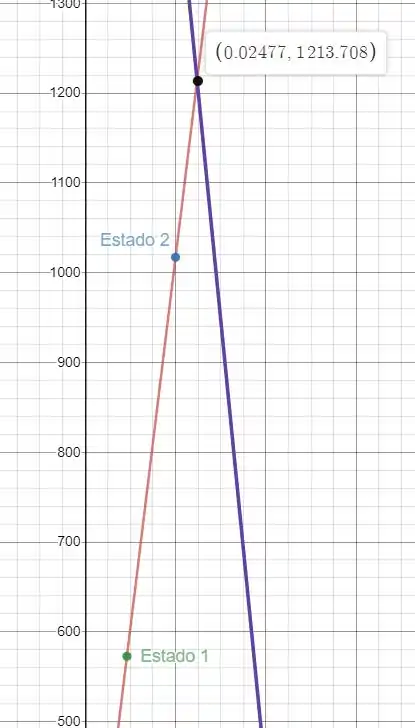
Com a reta roxa sendo a reta que veio da tabela para as pressões de e enquanto a vermelha é a reta do nosso conjunto
O eixo horizontal é o volume específico e a reta vertical a pressão em
Boladíssimo demais!
Passo 5
Aí para fechar essa questão falta o trabalho realizado e que será a mesma coisa que a área do gráfico, portanto ela será de:
Que é a área do triângulo que vai desde o estado até o estado , ou seja:
Ufa! Quanto trampo, vamos para mais depois de pegar um cafezinho por que nós merecemos depois dessa hahahah