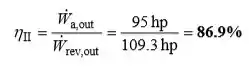Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 117
Gás argônio entra em uma turbina adiabática a e a uma taxa de , saindo a . Considerando que a potência produzida pela turbina é de , determine (a) a eficiência isentrópica e (b) a eficiência de segunda lei da turbina. Considere que a vizinhança está a .
Passo 1
Vamos lá, estudantes! Ana lise Existe apenas uma entrada e uma saída, logo . Tomamos a turbina isentrópica como o sistema, que é um volume de controle, uma vez que a massa atravessa o limite. (a) O balanço energético para este sistema de fluxo constante pode ser expresso na forma de taxa como
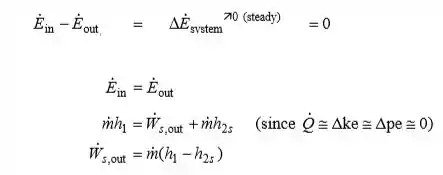
Das relações isentrópicas,
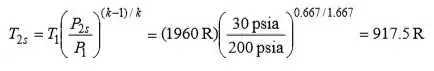
Então a potência de saída da turbina isentrópica torna-se
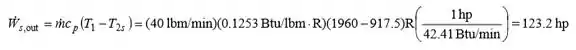
Passo 2
Então a eficiência isentrópica da turbina é determinada a partir,
(b) Usando a relação de balanço energético de fluxo constante acima, a temperatura real de saída da turbina é determinada como
A geração de entropia durante este processo pode ser determinada a partir de um balanço de entropia na turbina,
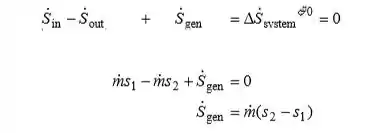
Onde,
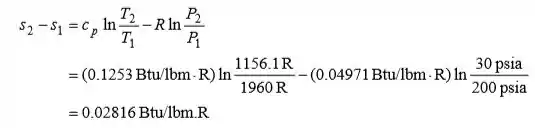
Passo 3
A exergia destruída durante um processo pode ser determinada a partir de um equilíbrio de exergia ou directamente a partir da sua definição,
Então o poder reversível e a eficiência da segunda lei tornam-se,
E,
