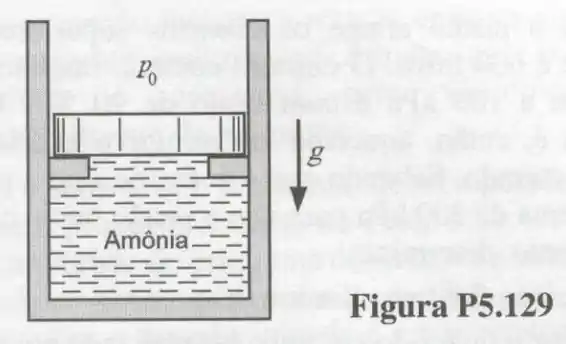
129- A mostra um conjunto cilindro-pistão que contém de amônia. Inicialmente, o pistão se encontra apoiado nos esbarros e a amônia apresenta e volume igual a .

A pressão interna necessária para movimentar o pistão é . Determine o calor transferido a amônia para que ela se torne vapor saturado. Determine, também, a temperatura final, o volume final e a transferência de calor neste processo.

Qual é a temperatura na amônia no instante em que o pistão desencosta dos esbarros?

Agora a dúvida que pode matar muita gente, como calcular a energia interna para calcular a transferência de calor sendo que eu somente tenho a entalpia na tabela , simples meu jovem gafanhoto, pela fórmula:

Na tabela a pressão absoluta e o volume específico, então pela tabela a temos:

Então a energia interna em estado saturado no estado inicial será:

Agora a energia interna evaporada:

Agora fazendo a energia inicial com a titulação do gás nós teremos:

Quando avançamos para o estado o gás é totalmente vapor então a titulação é , ou seja como nada se perde, massa não sai voando e o pistão está começando a desencostar nos esbarros então tanto massa, quanto volume específico e volume continuam o mesmo no estado final, ou seja:

Então pela tabela a temperatura cujo de evaporação seja será:

A ideia é pegar os volumes específicos que estão entre que estão entre e e dividir o intervalo desses volumes específicos dentro da diferença de e com isso saber em que posição está ao diminuir com o de menor temperatura (já que diminui a medida que a temperatura aumenta) com isso basta somar com .

Agora a energia interna da amônia superaquecida (pela tabela ) nesse estado final será de:

Então a energia interna será:

Pegando a entalpia para gás superaquecido e diminuindo a entalpia da referência a a vapor.

Então a transferência de calor será: