Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 5.Problemas - Ex. 132
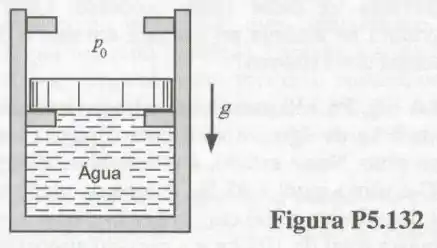
132- Considere o arranjo cilindro-pistão mostrado na . O pistão do arranjo pode deslizar livremente e sem atrito entre dois conjuntos de esbarros.
Quando o pistão repousa sobre os esbarros inferiores, o volume da câmara é , e quando o pistão atinge os esbarros superiores, o volume é . O cilindro contém, inicialmente, água a e com título de . Esse sistema é, então, aquecido até atingir o estado de vapor saturado.
Sabendo que é necessária uma pressão interna de para que o pistão inicie o seu movimento, determine:
- A pressão final no cilindro
- O calor transferido e o trabalho realizado em todo o processo
Passo 1
Eu queria começar essa questão dizendo que tudo vai dar certo, não importa as dificuldades que você esteja tendo nesse momento e essa questão é um dos muitos passos positivos e de vitórias que você dará na sua vida!
Para começar essa questão vamos entender como está o estado inicial da água quando o pistão está no estado inferior
E com essa pressão podemos ver pela tabela para a pressão de que para água saturada e (esse dado é da tabela )
Então o volume específico nesse estado será de:
E isso nos dá uma massa total de água de:
Use o volume em litros e saiba que essa massa é constante por todo o sistema.
A energia interna inicial será de:
Aqui usamos os dados da tabela e po e muito igual a então releve esse errinho hahaha
Além de que cuidado com as informações, a tabela é sobre vapor saturado então os dados que tem lá são os mesmos de vapor saturado.
Passo 2
Beleza, vamos avançar a questão e ver como esse conjunto se comporta
Para começar a gerar trabalho a água precisa estar a e não a como vimos anteriormente, então é realizado uma transformação isobárica aqui, e esse seria o estado 2 do conjunto. Não tem muito o que podemos falar sobre esse processo
Passo 3
Aí vem o estado 3 que onde temos realização de trabalho a mesma pressão de até chegar nos esbarros finais, então seu trabalho será de:
E nesse estado temos um volume específico de:
E pela tabela vemos que esse volume específico ainda não é o volume específico para termos vapor saturado que é de , então para que tenhamos de vapor saturado a pressão terá que aumentar um cadinho mais
Passo 4
Então para que tenhamos de vapor saturado no final, com a pressão no estado final deverá ser (com dados da tabela )
E isso nos dará uma energia interna nesse estado de:
Passo 5
Agora podemos começar respondendo as questões! Ele quer a pressão final do cilindro na letra , achamos que ela deve ser de , respondido! Toca ai!
Agora na letra , o trabalho. Somente temos o trabalho que vai do estado para o , e que é de , e essa parte tá respondida! Vem pro abraço meu engenheiro!!
Agora só falta o calor transferido, vem com o tio
Para calcular o calor somente precisamos do estado inicial e do estado final do sistema o que deixa o modelo de energia como:
Ou seja, a energia inicial do sistema acrescida de um calor fornecida a ela e subtraída do trabalho do sistema nos dá o estado final, e não importa o que acontece no meio, então
Então o calor transferido é de:
E assim temos o ponto cheio da questão, você aprovado e eu feliz :D Até a próxima