Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 5.Problemas - Ex. 137
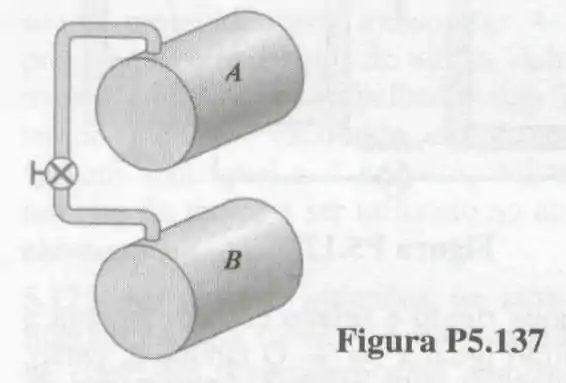
137- O tanque mostrado a apresenta volume interno igual a e contém ar a e . O tanque , indicado na mesma figura, contém de ar a e . A válvula é então aberta e espera-se que o ar atinja o equilíbrio térmico com o meio. Sabendo que o meio está a , determine a pressão do ar no estado final e a transferência de calor nesse processo.
Admita que o calor específico do ar é constante e igual aquele referente a temperatura de .
Passo 1
Você estaca dessa forma assim esses dias e tá desesperado para resolver o máximo de questão que dá para mandar bem na prova? Então vem comigo
Um bom primeiro passo é identificarmos muito bem os estados do sistema que estamos interessados, no caso vamos considerar dois sistemas, o do tanque e do tanque , então os estados iniciais nesses dois tanques são
No estado inicial de falta descobrirmos a massa e no estado o volume, então sabendo que na tabela a constante de gás perfeito do ar é de , então a massa no estado inicial de será:
E o volume inicial no tanque
Isso faz com que os volumes específicos iniciais sejam de:
Passo 2
Agora o estado é tal que a massa fique uniformemente distribuída no tanque ou seja o volume total passa a ser:
E a massa do ar passa a ser a soma das massas que tinham nos dois tanques
O que nos dá um volume específico no estado 2 de”
E a pressão no estado final do ar é de:
Pois nos é dito que a temperatura no tanque se equilibra com a temperatura ambiente que é de ou aproximadamente .
Note que encontrar essa pressão do ar no estado final já nos responde uma parte da questão :D meio ponto na prova já
Passo 3
Agora bem uma parte mais crítica da questão pois temos que conseguir modelar a energia nesse troço todo, onde tem uma transferência de ar de um tanque para o outro.
A questão pede a transferência de calor que há no processo e como ar estava parado nos dois tanques, se movimenta e depois se sedimenta de novo então não faz muito sentido falarmos em entalpia aqui.
Então podemos dizer que a energia interna presente nos dois tanques recebe uma parcela de calor para depois chegarmos no estado final, ou seja:
Isolando :
Nessa questão é um tanto difícil ver a energia interna pela tabela, pois temos muitas variáveis para analisar mesmo então vamos aproximar
Com pela tabela , então:
Essa tática de se usar é interessante principalmente quando se tem todas as temperaturas nos estados, senão tiver é melhor ir pela tabela.