Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 10.Problemas - Ex. 35
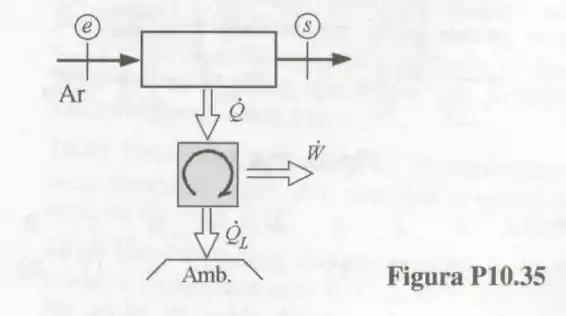
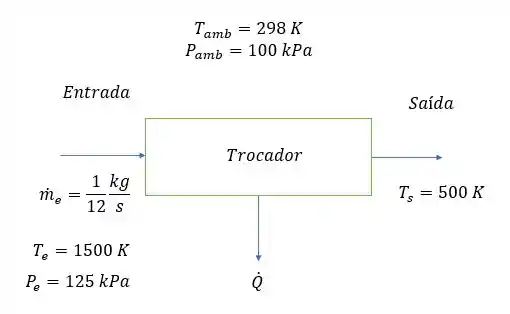
35- O trocador de calor mostrado na é alimentado com de ar a e .
Observe que o calor transferido do ar é fornecido para o motor térmico. O ar é descarregado do trocador a e o ambiente apresenta temperatura e pressão iguais a e .
Admitindo que a pressão no escoamento de ar é constante, determine a taxa de transferência de calor para o motor térmico e a potência que pode ser produzida nesse motor.
Passo 1
Primeiramente vamos notar que tem um dado que tá sangrando os olhos nessa questão, você sabe qual é?
Essa vazão de ar a me sangra os olhos, enquanto ela deveria estar com a unidade , vamos corrigir isso?
Ufa! Agora podemos dar prosseguimento na questão
Essas medidas exóticas me alteram um pouco, então eu sinto uma vontade enorme de já corrigir-las hahaha
Passo 2
Então vamos para a lógica da questão, eu tenho um trocador de calor de ar que serve de calor quente para um motor térmico realizar uma determinada potência (que é o que se pede nessa questão). Bem vamos então separar esse trocador de ar para ver se conseguimos tirar esse , então vem comigo
E como o calor é a diferença do calor do ar que tem na entrada com a saída e como não temos energia potencial e nem energia cinética envolvida então:
Já que a vazão se mantém a mesma, então vamos coletar esses dados de entalpia na tabela meus queridos alunos!
Nas condições que temos na entrada nós encontramos para a temperatura de :
E na saída encontramos para a temperatura de :
Portanto o calor que sai do trocador será de:
Note que a questão pedia esse calor, mas não podemos nos contentar com isso, nós queremos resolver a questão inteira
Passo 3
E se tínhamos até então uma questão de entalpia, entropia e todas essas coisas que vínhamos vendo nos capítulos anteriores, agora temos uma questão de motor térmico, onde temos , temos a temperatura ambiente, mas queremos saber a potência desse motor, então vamos com calma
Primeiramente vamos focar em achar essa que com ela nós conseguiremos encontrar o já é? Então vamos lá
O calor da fonte fria é jogado para o ambiente, e você sabe o que isso significa? Que a entropia gerada pelo sistema é representada por esse calor ‘’ jogada fora’’ com esse valor de , então a seguinte fórmula é válida
Como o sistema é reversível então , então:
Então pelos dados da tabela temos para e entropias padrões iguais a:
Só que não é necessariamente igual a sabe? A diferença de entropia pela entropia padrão normalmente é dada por:
Porém como a pressão no trocador de calor é constante então , então como , logo:
O que nos dá um de:
Passo 4
E agora feito todos esses preparativos podemos responder quando vale e para isso basta fazer:
E
Fizemos a questão todinha :D espero que você tenha entendido e até a próxima