Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 4.Problemas - Ex. 57
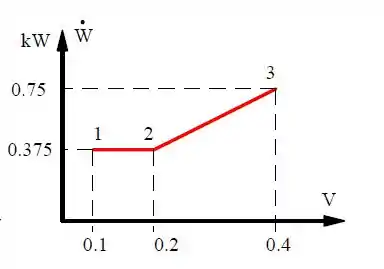
Admita que o processo no Problema 4.37 ocorra com uma taxa constante de variação de volume durante . Mostre a potência (taxa de trabalho) como função do tempo.
Passo 1
Vamos lá, pessoal! O enunciado nos pede a potência como função do tempo para o trabalho calculado no Problema 4.37. Lá nós tínhamos uma expansão de para , a uma pressão constante de , seguida de uma outra expansão de para com um aumento linear de pressão de para .
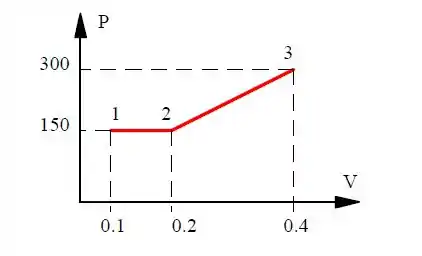
E, nesse processo, nós encontramos o trabalho e o diagrama :
Passo 2
Agora se o processo ocorre com uma taxa constante de variação de volume , durante , a potência é dada por:
Do diagrama , nós conseguimos estrai a variação de volume, que nos dá:
Então, quando ,
E quando a pressão sobe para ,
Plotando esses resultados, temos:
Resposta
Exercícios de Livros Relacionados
Um aquecedor de água tem área superficial de 3m 2 e está coberto com uma camada de isolante térmico. As temperaturas externa e interna da camada de isolante são, respectivamente, 75° C e 25° C . Saben
Ar, em um conjunto cilindro-pistão de pressão constante, está a 300k P a , 300K e com um volume de 0,1m 3 . O ar é então aquecido, durante 30s , até atingir 600K num processo com velocidade constante
Uma panela de aço, com condutividade térmica de 50W / m K , contém água líquida a 15° C . A espessura da panela é uniforme e igual a 5m m e o diâmetro da panela é de 20c m . A panela está colocada sob
Devido a uma falha no contato da porta, a pequena lâmpada de iluminação interna de uma geladeira ( 25W ) permanece acesa com a porta fechada. As paredes da geladeira têm isolamento térmico limitado e,
A temperatura da superfície de uma tora da madeira, queimando numa lareira, é de 450 ° C . Admita que a emissividade da superfície da tora é igual a 1 (corpo negro perfeito) e determine a taxa de emis