Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 53
A turbina de um ciclo de potência é alimentada com vapor d’água a e . A pressão na seção de descarga da turbina é . A eficiência isoentrópica desta turbina é igual a e a potência produzida na turbina é . Determine a vazão em massa de água no ciclo e a taxa de transferência de calor no condensador. Qual é a eficiência térmica deste ciclo? Compare a eficiência térmica deste ciclo com um de Carnot que opera entre as temperaturas máxima e mínima do ciclo.
Passo 1
Oi, tudo bem? Vamos analisar essa questão!
Neste exercício nós temos uma turbina trabalhando em um ciclo de potência. Temos que o fluido de trabalho é o vapor d’água que entra na turbina a e e sai a . Sabemos que a turbina é real pois temos o valor da sua eficiência isoentrópica.
Queremos A vazão em massa de água do ciclo, a taxa de transferência de calor no condensador e a eficiência térmica do ciclo. Depois que descobrirmos a eficiência térmica, temos que comparar com a eficiência de Carnot.
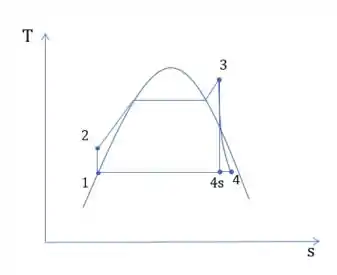
Um ciclo de potência a vapor é representado pelo seguinte diagrama T-s:
Passo 2
O caminho representa o processo isoentrópico realizado pela turbina e o processo real.
A partir da análise da tabela de propriedades termodinâmicas para o vapor de água, com e , temos que:
Como foi dito anteriormente, o processo é isoentrópico, portanto:
Como na saída da turbina temos que:
Podemos utilizar o valor da entropia e da pressão do estado para descobrir o título e a entalpia específica. Primeiro vamos descobrir o título correspondente do estado :
A entalpia específica será:
Passo 3
Sabendo a entalpia específica do estado podemos encontrar o trabalho isentrópico da turbina:
Como temos a eficiência isentrópica, podemos encontrar o trabalho específico real realizado pela turbina:
O exercício nos disse que a potência produzida na turbina é de , portanto o fluxo mássico do fluido será:
Passo 4
O exercício também nos pede a taxa de transferência de calor do condensador. O processo real realizado pelo condensador é representado por . Portanto, temos que:
Podemos descobrir o valor da entalpia do estado a partir do trabalho real:
A entalpia do estado é dada na tabela de propriedade termodinâmica para o líquido saturado a . Portanto, o calor específico transferido pelo condensador é de:
Como queremos a taxa de transferência relacionada ao calor transferido pelo condensador, temos que multiplicar pelo fluxo mássico:
Passo 5
A eficiência térmica é dada pela razão entre o trabalho líquido e o calor fornecido, ou seja, da caldeira:
O trabalho líquido é dado pela subtração do trabalho produzido pelo trabalho gasto, ou seja, trabalho de turbina menos o trabalho da bomba:
A eficiência térmica será:
A eficiência de Carnot é dada pela seguinte equação:
Onde é a temperatura da fonte fria e a temperatura da fonte quente.
Temos que:
Podemos notar que a eficiência de Carnot é maior que a eficiência térmica real do sistema. Isso se deve pelo fato de a máquina de Carnot ser ideal, enquanto nosso sistema é real.
Ufa, terminamos mais uma questão. Conseguimos te ajudar? Responde Aí!!