Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 3.Problemas - Ex. 69
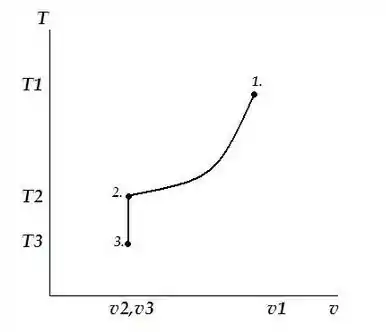
Um arranjo cilindro-êmbolo contém, inicialmente, amônia a e . A amônia é resfriada a pressão constante até atingir o estado de vapor saturado (estado 2), quando então o êmbolo é travado por um pino. O resfriamento continua até que a temperatura atinja (estado 3). Mostre, nos diagramas e , os processos do estado 1 para o 2 e do estado 2 para o estado 3.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Nós temos os seguintes dados fornecidos pelo enunciado
Da tabela B.2.1 (Amônia saturada), com a temperatura correspondente , nós podemos encontrar a pressão de saturação e o volume específico:
Quando estamos a
Usando o método de interpolação linear, podemos calcular a temperatura de saturação do estágio 2 correspondentes à pressão
Passo 2
Também podemos calcular o volume específico do estágio 2 pelo método de interpolação linear:
Da tabela de Amônia Saturada B.2.1. correspondente a podemos encontrar a pressão do estágio 3:
O processo 2-3 é o processo de volume constante:
Passo 3
O diagrama é igual a
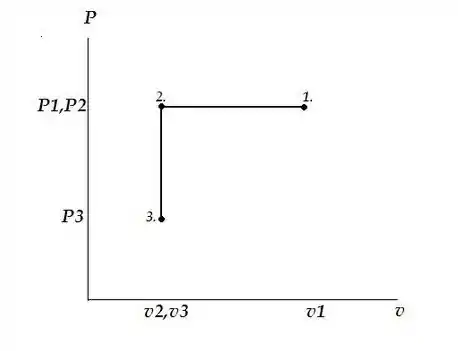
E o diagrama
Resposta
