Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 28
Um automóvel é acelerado do repouso a em . A energia transferida para o automóvel seria diferente se ele fosse acelerado à mesma velocidade em ?
Passo 1
A questão compara dois casos. Em um caso, um automóvel recebe uma energia e sai do repouso (velocidade ), alcançando uma velocidade de em . Em outro caso, o mesmo automóvel recebe uma energia e sai do repouso, alcançando uma velocidade de em . A questão quer saber se a energia transferida ao carro no primeiro caso é igual ou diferente da energia transferida ao carro no segundo caso.
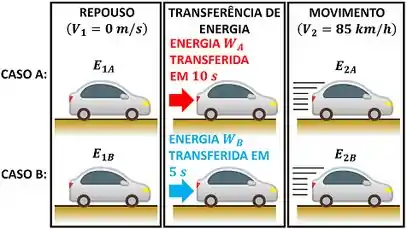
e são a energia do carro em repouso no caso A e no caso B respectivamente e e são a energia do carro a no caso A e no caso B respectivamente.
Para comparar as energias transferidas e , precisamos calcular esses dois termos. é a diferença entre a energia final do carro e a energia inicial do carro .
é a diferença entre a energia final do carro e a energia inicial do carro .
Ou seja, para calcular e comparar e vamos precisar aprender a calcular , , e . Faremos esse entendimento no próximo passo.
Passo 2
Quando o carro está em repouso , tanto no caso A quanto no caso B, sua energia cinética vale zero. Isso quer dizer que:
Quando o carro está em movimento, as energias cinéticas do carro são calculadas através das equações abaixo.
Como a massa do carro nos dois casos são iguais e a velocidade do carro nos dois casos são iguais, as energias finais e são iguais.
No próximo passo vamos substituir essas energias na fórmula de e .
Passo 3
Substituindo os novos dados nas equações de e somos capazes de calcular esses dois termos e, enfim, comparar esses dois termos.
Vemos então que:
Ou seja, a energia transferida para o automóvel no caso A é igual à energia transferida para o automóvel no caso B . Isso quer dizer que o tempo de transferência de energia não tem influência na quantidade de energia que é necessária para fazer o automóvel sair do repouso e passar a se mover a uma certa velocidade.
Resposta
A energia transferida para o automóvel no caso A é igual à energia transferida para o automóvel no caso B .