Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 8.Problemas - Ex. 73
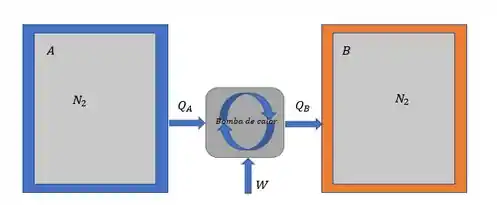
Em cada um dos dois tanques rígidos, mostrados na Fig. P8.73, estão contidos de nitrogênio gasoso a e . Os tanques são então conectados termicamente a uma bomba de calor reversível, que aquece um tanque e resfria um outro sem transferência de calor com o meio ambiente. Quando um tanque é aquecido a , o processo para. Determine os valores finais de e em ambos os tanques e o trabalho recebido pela bomba de calor, considerando calores específicos constantes.
Passo 1
Fala, galera! Nessa questão nós temos uma bomba de calor transferindo calor para dois tanques, mantendo um quente e um frio. Nesse sistema nós temos uma massa de que é e as propriedades do estado inicial:
Vamos chamar de o tanque frio e de o tanque quente.
Como o tanque é o que está recebendo calor, ao final do processo sua temperatura será:
O volume e a massa são constantes no tanque, então o trabalho realizado nesse volume de controle é nulo. Dessa forma, o calor transferido, dado pela 1ª lei da termodinâmica, vai ser igual a energia interna:
Mas a energia interna gerada pelo fluido é dada por:
Substituindo isso na equação da 1ª lei:
Dessa forma, usando os dados do enunciado podemos determinar o calor transferido no tanque:
E a pressão final no tanque pode ser calculada utilizando a lei dos gases, com o volume constante:
Substituindo os valores:
Passo 2
Como o processo é reversível, nossa variação de entropia é nula. Então a entropia no tanque quente é igual à do tanque frio:
Logo,
Usando a propriedade de logaritmo:
Portanto, isolando e substituindo os valores:
De posse da temperatura, podemos encontrar a pressão:
Passo 3
O calor retirado da fonte fria através da bomba é de:
Substituindo os valores:
O sinal negativo indica que o calor foi retirado do sistema.
O calor fornecido ao tanque será o trabalho da bomba mais o calor retirado do tanque :
É isso, galera, valeu! 😉.