Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 82
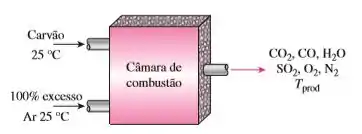
Um carvão da Pensilvânia (Estados Unidos), cuja análise final (em massa) corresponde a 84,36% de C, 1,89% de , 4,40% de , 0,63% de , 0,89% de S e 7,83% de cinzas (não combustíveis) é queimado em uma caldeira industrial com 100% de ar em excesso. Essa combustão é incompleta, e 3% (em volume) de carbono nos produtos formam monóxido de carbono. Qual é o impacto da combustão incompleta da temperatura adiabática de chama (em °C), em comparação a um processo de combustão completa? Despreze o efeito do enxofre no balanço de energia.
Passo 1
Vamos assumir que:
Existem condições operacionais estáveis.
Ar e gases de combustão são gases ideais.
As energias cinética e potencial são desprezíveis.
Não há interações de trabalho.
A câmara de combustão é adiabática.
As massas molares de e ar são 12, 2, 28, 32, 32 e 29 kg / kmol, respectivamente (Tabela A-1).
Passo 2
Consideramos 100 kg de carvão para simplificar. Observando que as porcentagens de massa neste caso correspondem às massas dos constituintes, os números molares do constituinte do carvão são determinados como sendo:
O número molar da mistura e as frações molares são:
As cinzas consistem na matéria não combustível do carvão. Portanto, a massa do conteúdo de cinzas que entra na câmara de combustão é igual ao conteúdo de massa que sai. Desconsiderando esse componente que não reage por simplicidade, a equação da combustão pode ser escrita como:
De acordo com o balanço de espécies,
Balanço de carbono:
Balanço de :
Balanço de
Balanço de
Balanço de
Substituindo:
Sob condições de fluxo constante, o balanço energético aplicado na câmara de combustão com Q = W = 0, temos:
Passo 3
Das tabelas:
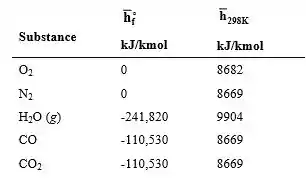
A temperatura do produto é obtida a partir de uma solução de tentativa e erro. Um primeiro palpite é obtido dividindo o lado direito da equação pelo número total de moles, o que gera:
Gerando:
E então teremos:
Esse valor de entalpia corresponde a cerca de 1600 K para . Observando que a maioria das moles é , o estará próximo de 1600 K, mas um pouco abaixo dele, devido ao maior calor específico do .
À 1500K:
À 1520K:
Por extrapolação:
Passo 4
Repetimos os cálculos para a combustão completa agora:
A equação de combustão neste caso pode ser escrita como:
De acordo com o balanço de espécies,
Balanço de
Balanço de
Balanço de
Balanço de
Balanço de
Substituindo:
Sob condições de fluxo constante, o balanço energético aplicado na câmara de combustão com Q = W = 0, temos:
Das tabelas:
Então,
A temperatura da produção é obtida a partir de uma solução de tentativa e erro. Um primeiro palpite é obtido dividindo o lado direito da equação pelo número total de moles, o que gera
Esse valor de entalpia corresponde a cerca de 1600 K para . Observando que a maioria das moles é , o estará próximo de 1600 K, mas um pouco abaixo dele, devido ao maior calor específico do .
À 1500K:
À 1520K:
Por extrapolação: