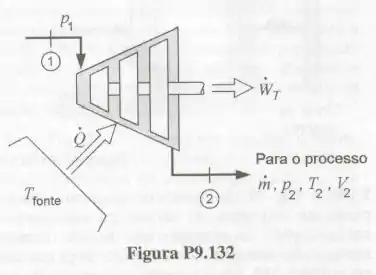
Um certo processo industrial requer de ar a e . Além disso, a velocidade deste escoamento deve ser igual a . Propõe-se utilizar a turbina especial mostrada na Fig. P9.132, que é alimentada com um escoamento de ar que apresenta pressão igual a , para fornecer este insumo. O processo de expansão na turbina pode ser considerado reversível e politrópico (com expoente politrópico igual a ).

a) Qual é a temperatura do ar na seção de alimentação da turbina?

b) Determine a potência produzida pela turbina e a taxa de transferência de calor no processo.

c) Determine a taxa líquida de aumento de entropia se a transferência de calor for realizada de uma fonte que apresenta temperatura mais alta do que àquela do ar na seção de alimentação da turbina.

Letra a)

Calculando a temperatura do ar na seção de alimentação da turbina.

Como temos um gás ideal em um processo politrópico, podemos utilizar a seguinte equação:

Substituindo os dados:

Letra b)

Determinando a potência produzida pela turbina e a taxa de transferência de calor no processo.

Pela equação da 1ª Lei, temos:

Sendo um processo reversível e politrópico e realizando algumas considerações, temos:

Modificando a equação e desconsiderando a velocidade de entrada:

Substituindo os dados:

Assim, a potência se dá:

Calculando a taxa de transferência de calor:

Substituindo os dados, temos:

Determinando a taxa líquida de aumento de entropia.

Pela 2ª Lei:

Sendo:

Como:

Então:

Substituindo os dados:

E assim acabamos mais uma questão, até a próxima!