Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 35
Uma comporta deslizante está montada na barragem de uma represa que apresenta profundidade igual a . Admita que existe um furo, com diâmetro de , posicionado na parte inferior da comporta. Sabendo que a temperatura da água que escoa pelo furo é e desprezando qualquer variação de energia interna da água durante o escoamento através do furo, determine a velocidade da água na seção de descarga do furo e a vazão em massa do escoamento através do furo.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para esta questão vamos aplicar a equação do balanço de energia. Temos que escolher dois pontos de interesse, para aplicar. Observe o seguinte esboço:
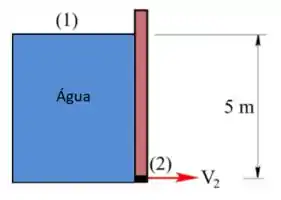
Teremos então com ponto a superfície da água represada e como ponto o furo da comporta.
E para esse arranjo é importante ter em mente algumas especificidades, como a velocidade no ponto que pode ser desprezada, pois como estamos trabalhando com um reservatório muito grande, se comparada com a velocidade de saída, a velocidade de entrada se torna desprezível.
Temos então a seguinte equação:
Onde:
Passo 2
De posse destas informações, vamos às considerações.
Como dito anteriormente, temos que:
Vamos considerar que e .
Outro fato importante é de que a entalpia específica nos pontos e é a mesma. Isso acontece pois estão sob efeito da mesma pressão, atmosférica, e as variações nas energias internas devem ser desprezadas.
Portanto, teremos o seguinte arranjo:
A velocidade do escoamento na saída será:
Substituindo os valores, temos que:
Passo 3
O exercício também nos pede a vazão mássica na saída. Temos a seguinte equação:
O volume específico, é encontrado a partir da tabela de propriedades termodinâmicas da água saturada para e vale:
A área é dada por:
A vazão mássica será: