Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 42
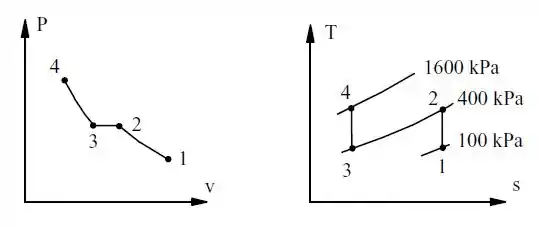
Um compressor de ar de dois estágios possui um refrigerador entre os estágios (intercooler), conforme mostrado na Fig. P11.42. O estado na entrada é de e , e a pressão final de saída é de . Considere que o ar é resfriado, a pressão constante, até a temperatura de entrada, . Pode-se mostrar que a pressão ótima, que minimiza o trabalho total no compressor, é . Determine o trabalho no compressor e a transferência de calor no resfriador, por unidade de massa de ar, para o ótimo.
Passo 1
Fala, galera! Vamos resolver essa questão.
Galera, a primeira coisa é a fazer é se atentar para o fato de que a pressão ótima para o resfriador intermediário é dada por:
Substituindo os valores do enunciado:
E aí da tabela, nós conseguimos extrair a entalpia e a entropia:
Passo 2
Beleza, galera. Agora vamos por etapas. Para o compressor no estágio 1, temos:
Com isso, podemos usar a equação:
Que nos fornece os valores:
Logo, o trabalho será:
Passo 3
Para o resfriador, temos:
Logo, a transferência de calor na saída será:
Passo 4
Agora para o compressor no estágio 2, temos:
Logo,
Substituindo na equação de entropia:
Então nós temos:
E dessa forma,
E concluímos o exercício! 😉