Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 44
Um compressor de duplo estágio, em um ciclo de turbina a gás, leva o ar atmosférico do estado inicial e para , no primeiro estágio, e, em seguida, resfria o ar até em um resfriador intermediário, mantendo a pressão constante. O segundo estágio comprime o ar até . Considere que ambos os estágios são adiabáticos e reversíveis. Determine o trabalho específico total para os estágios do compressor. Compare o resultado obtido com o trabalho específico para o caso de não existir resfriador (isto é, um único estágio de compressão de até ).
Passo 1
Fala, galera! Vamos resolver essa questão.
Galera, primeiro vamos extrair alguns dados do enunciado. Temos:
Ambos os estágios são adiabáticos e reversíveis, então a entropia é sempre constante.
Passo 2
Beleza, galera. Agora vamos por etapas. Pela equação de energia, temos para o compressor no estágio 1:
Como processo tem entropia constante, , e podemos verificar quem é por meio da relação:
Substituindo isso na equação do trabalho:
Passo 3
Vamos repetir o processo para verificar o trabalho e a temperatura no estágio 2 do compressor:
Como processo tem entropia constante, , e podemos verificar quem é por meio da relação:
Substituindo isso na equação do trabalho:
Passo 4
Finalmente, temos o trabalho específico total:
Perceba que o resfriador reduz o trabalho para o estágio 2, porque a temperatura é menor. Caso não exista o resfriador, nós ainda temos um processo adiabático reversível, com entropia constante, que nos fornece:
Substituindo isso na equação do trabalho:
Esta redução do trabalho pelo resfriador, pode ser vista na área sombreada do diagrama :
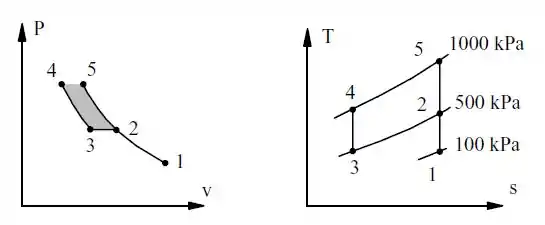
E concluímos o exercício! 😉