Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 50
Um queimador posterior, em um motor a jato, injeta e queima combustível após a turbina, aumentando assim a pressão e a temperatura por meio da energia de combustão. Admita uma condição padrão de e após a turbina e entrando no bocal, cuja descarga é de . Considere que o queimador adiciona ao estado padrão com um aumento na pressão para o mesmo volume específico e despreze quaisquer efeitos de montante sobre a turbina. Determine a velocidade de saída do bocal antes e após o acionamento do queimador posterior.
Passo 1
Fala, galera! Vamos resolver essa questão.
Vamos começar dando uma olhada no diagrama do processo:
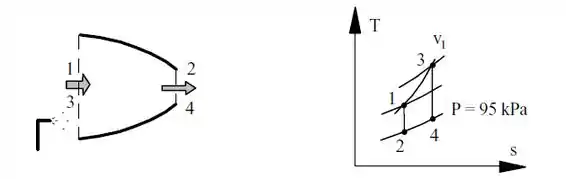
Assumindo que o processo no bocal é adiabático e reversível, temos entropia constante e podemos usar a relação:
Podemos calcular a velocidade de saída do bocal por meio da equação de energia, na forma:
Passo 2
Adicionando a energia do queimador e considerando o volume constante, a equação de energia nos fornece:
Como o volume não se altera, temos:
Após o acionamento do queimador, temos uma expansão adiabática reversível, então:
Usando novamente a equação de energia para determinar a velocidade, temos:
E concluímos o exercício. Valeu, galera! 😉