Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 35

Um conjunto cilindro-pistão, com área da seção transversal igual a 0,25   m 2 , opera a pressão constante e contém água. Inicialmente, a água se encontra como vapor saturado a 200   k P a e a distância entre o pistão e o fundo do cilindro é 0,1 m . Transfere-se calor para a água até que sua temperatura se torne igual a 200 ° C . Determine o trabalho realizado nesse processo.

Passo 1

Ooi pessoal, tudo certo? Bora resolver.

Seguinte a situação que temos é esta aqui:

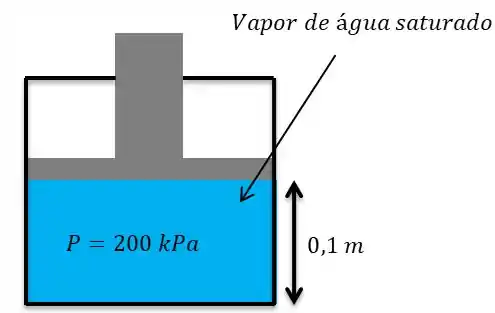
E temos um processo de aumento de temperatura de 200 ° C .

Precisamos determinar o trabalho feito deste processo.

Como o nosso sistema é um sistema cilindro-pistão temos que a variação do volume específico é proporcional a variação da altura que o nosso pistão se encontra do fundo do cilindro, isso é importante saber, pois, na fórmula que utilizaremos para calcular o trabalho precisaremos saber o volume no estado final após o aumento de 200 ° C .

Passo 2

Seguindo a ideia do passo 1, vamos determinar o a altura do pistão no estado final, que ao multiplicarmos pela área teremos a o volume ocupado no estado final.

A equação de proporção é definida por:

h 2 h 1 = v 2 v 1

Agora os volumes específicos serão determinados pelas tabelas:

Estado inicial tínhamos vapor saturado, portanto, utilizaremos B . 1.2 . Procurando o volume de vapor com a pressão de 200   k P a :

v 1 = v V = 0,8857   m 3 / k g

Estado final, sabemos que vapor saturando ao aumentar sua temperatura fica vapor superaquecido, devido a isto, utilizaremos B . 1.3 . Procurando com pressão de 200 k P a e temperatura de 200 ° C , temos:

v 2 = 1,0803   m 3 / k g

Passo 3

Com todos os dados em mãos, bora substituir na fórmula:

h 2 h 1 = v 2 v 1

h 2 = v 2 v 1 ∙ h 1 = 1,0803   0,8857   ∙ 0,1 = 0,122   m

Passo 4

Bem, como a pressão do nosso processo é constante, podemos utilizar a fórmula em que o trabalho é integrável, que é definida por:

W = ∫ P   d V = P ∙ Δ V

W = P ∙ A ∙ h 2 - h 1

Substituindo os valores, temos que o trabalho foi de:

W = 200 ∙ 0,25 ∙ 0,122 - 0,1 = 1,1   k J

É isso pessoal, valeu.

Resposta

W = 1,1   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o P r o b .4 – 16 . Usando o EES (ou outro programa), trace um gráfico do processo descrito no problema em um diagrama P - V e investigue o efeito do expoente politrópico n no trabalho de
32 Um aquecedor de ambientes a vapor, localizado numa sala a 25°C, é alimentado com vapor saturado a 110 kPa. As válvulas de alimentação e descarga são fechadas e espera-se para que a temperatura da á
31 Um conjunto cilindro – pistão opera a pressão constante e, inicialmente, contém 0,2 kg de vapor saturado de água a 400 kPa. O conjunto é resfriado até que o volume da água se torne igual a metade d
Um conjunto cilindro-pistão sem atrito contém 5,0k g de vapor de refrigerante R - 134 a a 1000k P a e 140 ° C . O sistema é resfriado a pressão constante, até que o refrigerante apresente título igual
Considere o conjunto cilindro-pistão descrito no Problema 2.57 . Inicialmente, a altura da camada de água apoiada no pistão é igual a 5m e a temperatura da água é 20 ° C . A área da seção transversal