Considere um arranjo cilindro-pistão como o mostrado na Fig. P4.64. Inicialmente, o arranjo contém 1k g água líquida a 300k P a e 20 ° C e o pistão não está encostado nos esbarros. O volume interno do conjunto é 0,002m 3 quando o pistão está encostado nos esbarros. A água é então aquecida até que a pressão atinja 600k P a . Determine o trabalho realizado no processo e também o volume da água no estado final.

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 67

Considere um arranjo cilindro-pistão como o mostrado na Fig. P4.64. Inicialmente, o arranjo contém água líquida a e e o pistão não está encostado nos esbarros. O volume interno do conjunto é quando o pistão está encostado nos esbarros. A água é então aquecida até que a pressão atinja . Determine o trabalho realizado no processo e também o volume da água no estado final.

Passo 1

Fala galera, tudo bom? Bora resolver esta questão comigo?

Galera temo que determinar o volume no estado final e o trabalho realizado neste processo.

Para sabermos se o pistão no estado final está encostando nos esbarros basta compararmos a pressão inicial, que iremos considerada a pressão mínima para levantar o pistão, com a pressão final.

Temos que , portanto o nosso pistão está encostado nos esbarros e o volume final o enunciado já nos disse:

Passo 2

Para o trabalho teremos que aplicara fórmula da área integrável do trabalho. Vamos ilustrar essa área:

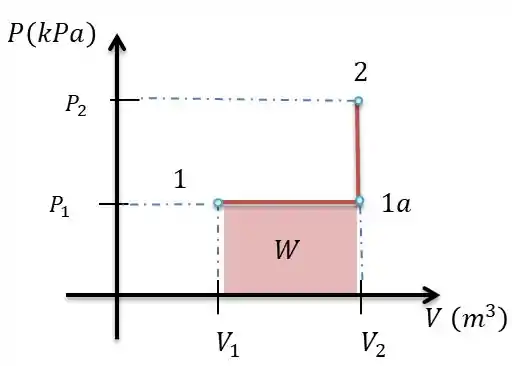
Note que o momento é o momento em que temos o volume final, mas a pressão ainda não se alterou, após este momento a pressão altera e o volume é constante, devido o volume ser constante a derivada de uma constante é zero, logo:

Passo 3

Com a fórmula do trabalho modelada, temos que encontrar o volume inicial.

Como temos água líquida e a seguinte condição de estado e , olhando na tabela :

Passo 4

Substituindo as variáveis no trabalho, temos:

Multiplicando pela massa:

É isso galera fecho.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma massa passando por um processo politrópico onde a pressão é diretamente proporcional ao volume ( n = - 1 ). O processo começa com P = 0 , V = 0 e termina com P = 600 k P a e V = 0,01m 3

Determine o trabalho específico no Problema 3.27.

A pressão no ar contido num conjunto cilindro-pistão mola, semelhante ao mostrado na figura P3.60, é linear com o volume e é dada por P = A + B V . No estado inicial, P = 150k P a e V = 1 l , e no est

Um conjunto cilindro-pistão contém Butano, C 4 H 10 , a 300° C e 100k P a com um volume de 0,02m 3 . O gás é então comprimido lentamente em um processo isotérmico até 300k P a . a. Mostre que é razoáv

Um conjunto cilindro-pistão contém 0,5k g de ar a 5 00k P a e 500K . O ar expande em um processo tal que a pressão decresce linearmente com o volume até um estado final de 100k P a e 300K . Determine