Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 44
Um conjunto cilindro-pistão contém de ar. Inicialmente, a temperatura e a pressão no ar são iguais a e . O ar então expande, num processo onde a pressão cai linearmente com o volume até que a temperatura e a pressão no ar se tornem iguais a e . Determine o trabalho realizado no processo.
Passo 1
Fala pessoal, beleza?
Temos ar como fluido de trabalho, e temos que determinar o trabalho realizado no processo.
Bem a fórmula de trabalho integrável é a seguinte:
Para determinar o nosso trabalho, antes, teremos que calcular o volume no estado 1 e estado 2.
E para determinar esses volumes teremos que assumir que o ar é um gás ideal, com essa licença podemos utilizara fórmula do gás ideal:
Passo 2
Calculando o volume para o estado inicial:
Olhando na tabela encontraremos . Substituindo os valores:
Repetindo o processo só que para temperatura e pressão no estado final:
Passo 3
Com os volumes calculados, ficou tranquilo calcular o trabalho. Vamos montar o diagrama para termos uma noção melhor de como podemos calcular o trabalho.
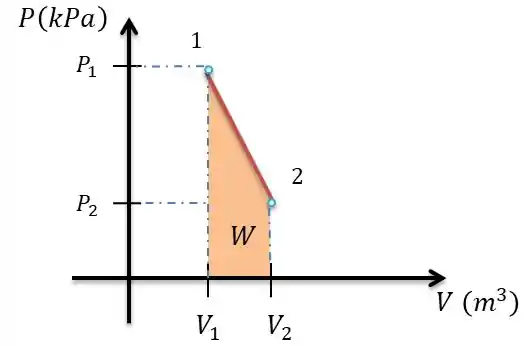
Note que a variação da pressão com o volume é uma variação linear, portanto, a área sobre a reta deste gráfico resultará no nosso trabalho.
A área que temos configura um trapézio, a área de um trapézio é a soma das duas bases dividia por 2 e multiplicado por sua altura.
É isso pessoal, valeu.