Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 58
Considere um ciclo de Rankine regenerativo ideal com dois aquecedores de água de alimentação, um fechado e outro aberto. Vapor entra na turbina a 10 Mpa e 600 °C e é descarregado para o condensador a 10 kPa. Vapor é extraído da turbina a 1,2 Mpa, para o aquecedor de água de alimentação fechado, e a 0,6 Mpa, para o aquecedor aberto. A água de alimentação é aquecida até a temperatura de condensação do vapor extraído no aquecedor de água de alimentação fechado. O vapor extraído sai do aquecedor de água de alimentação fechado como líquido saturado, que depois é estrangulado para o aquecedor de água de alimentação aberto. Mostre o ciclo em um diagrama T-s que inclua as linhas de saturação e determine (a) o fluxo de massa do vapor na caldeira para uma potência líquida de 400 MW e (b) a eficiência térmica do ciclo.
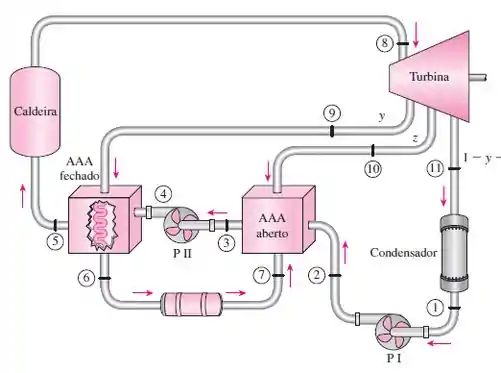
Passo 1
Vamos começar desenhando o diagrama T-s para o sistema, pois ele também vai nos ajudar a encontrar os pontos de interesse e suas propriedades logo mais, então, teremos:
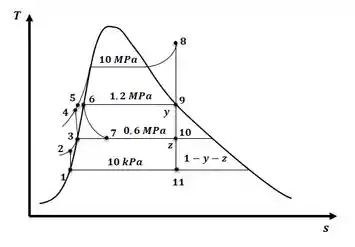
Beleza! Então agora o que temos que fazer é pegar o valor das propriedades nos pontos de interesse, então teremos:
Como do ponto 6 para o ponto 7, temos um mecanismos de estrangulamento, sabemos que podemos considerá-lo isoentálpico, então temos:
Sabemos também, através do enunciado, e podemos visualizar isso através do diagrama T-s, que:
Então, seguindo com as propriedades, temos:
Então, calculado o título para o ponto 11, temos:
Dessa forma, a entalpia será:
Passo 2
Agora vamos calcular os trabalhos específicos das bombas para descobrir as entalpias nos pontos de saída de cada uma delas, então, começando pela bomba 1, temos:
E, com isso, aplicando o equilíbrio de energia para a bomba 1, temos:
Da, mesma forma, calculando o trabalho da bomba 2, temos:
E, com isso, aplicando o equilíbrio de energia para a bomba 2, temos:
Passo 3
Agora nós vamos aplicar o balanço de energia para o regenerador fechado do passo 1, então, temos:
Nesse caso temos regime permanente, então , dessa forma a equação se torna:
E analisando o regenerador fechado, teremos:
No entanto, olhando o diagram do passo 1, sabemos que:
E, com a relação mássica para o regenerador fechado, a equação se torna:
Substituindo os valores conhecidos, temos:
Agora, aplicando o mesmo raciocínio, só que para o regenerador aberto, temos:
E analisando o regenerador aberto, teremos:
E, com a relação mássica e para o regenerador aberto, a equação se torna:
Substituindo os valores conhecidos, temos:
Agora podemos aplicar o equilíbrio de energia para a caldeira e descobrir o calor fornecido ao sistema, então, teremos:
E, da mesma forma, aplicando o equilíbrio para o condensador, usando as frações mássicas descobertas anteriormente, temos:
Substituindo os valores conhecidos, temos:
Com, esses dois valores, conseguimos encontrar o trabalho líquido do sistema, que será:
E, finalmente, com esse valor de trabalho líquido específico, como já temos a potência produzida pela turbina, podemos encontrar a vazão mássica através de:
Passo 4
E, agora, usando também os calores que entram e saem do sistema encontrados no passo 3, podemos encontrar a eficiência do sistema através de:
Então, substituindo os valores conhecidos, temos: