Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 49
O ciclo de Rankine regenerativo ideal com um aquecedor de água de alimentação aberto usa água como fluido de trabalho. A entrada da turbina é operada a 500 psia e 600 °F, e o condensador, a 5 psia. Vapor a 40 psia é fornecido ao aquecedor de água de alimentação aberto. Determine o trabalho produzido pela turbina, o trabalho consumido pelas bombas, o calor rejeitado no condensador para esse ciclo por unidade de fluxo através da caldeira.
Passo 1
Para nos ajudar a visualizar o problema, vamos utilizar o diagrama do ciclo Rankine com regenerador aberto fornecido nessa seção do livro:
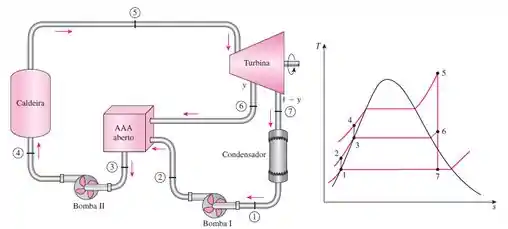
Primeiro temos que converter os dados fornecidos para podermos obter os dados nas tabelas termodinâmicas:
Tá legal! Agora vamos pegar os dados nas tabelas termodinâmicas referentes aos pontos que temos informações, então, temos:
Passo 2
Com os dados coletados no passo 1, podemos calcular o trabalho específico da bomba 1, então, temos:
Substituindo os valores conhecidos, temos:
Agora então podemos aplicar o equilíbrio de energia específica para a bomba 1 para descobrir o valor da entalpia em 2, de modo que teremos:
Substituindo os valores conhecidos, temos:
Agora, da mesma forma, vamos calcular o trabalho específico da bomba 2:
Substituindo os valores conhecidos, temos:
E, com isso, agora, podemos encontrar a entalpia no ponto 4 aplicando o equilíbrio de energia específico para ela:
Substituindo os valores conhecidos:
Então, o trabalho total requerido pelas bombas será:
Passo 3
Agora faltam os dados referentes aos pontos 6 e 7, dessa forma, sabendo que a expansão na turbina é isentrópica, temos , então, para o ponto 6, teremos:
Para a pressão , pegando os dados de interesse na tabela, temos:
Dessa forma, a entalpia no ponto 6 será:
Da mesma forma, para o ponto 7 a , temos:
E a entalpia nesse ponto será:
Passo 4
Agora aplicando o balanço de energia para o regenerador, temos:
Como temos regime permanente, então a energia que entra é igual a energia que sai, então:
Sabendo que não temos calor ou trabalho entrando ou saindo do sistema e que podemos desprezar as variações de energia cinética e potencial, dessa forma a equação do balanço de energia se torna:
De acordo com a proporção mássica ilustrada no diagrama do passo 1, podemos reescrever a equação como:
Substituindo os valores conhecidos, temos:
Com isso, podemos aplicar o equilíbrio de energia específico para a turbina e assim obter seu trabalho específico:
Substituindo os valores conhecidos, temos:
Passo 5
Agora, o calor rejeitado no condensador pode ser encontrado aplicando um equilíbrio de energia específica para o mesmo, então, teremos:
Substituindo os valores conhecidos, temos:
Apesar do enunciado não pedir, vamos calcular a eficiência térmica desse sistema, pois precisaremos desse dado no problema 10.50. Então, para isso, precisamos encontrar o calor que entra no sistema pela caldeira, aplicando um balanço de energia específica na caldeira, temos:
Substituindo os valores conhecidos, temos:
Então, a eficiência térmica do sistema será: